Appex 06 – tidymodels

STA 363 - Spring 2023

Set up

Login to RStudio Pro

• Note: if you are off campus, you will need to use a VPN to connect
• Go to rstudio.deac.wfu.edu

Step 1: Create a New Project

Click File > New Project

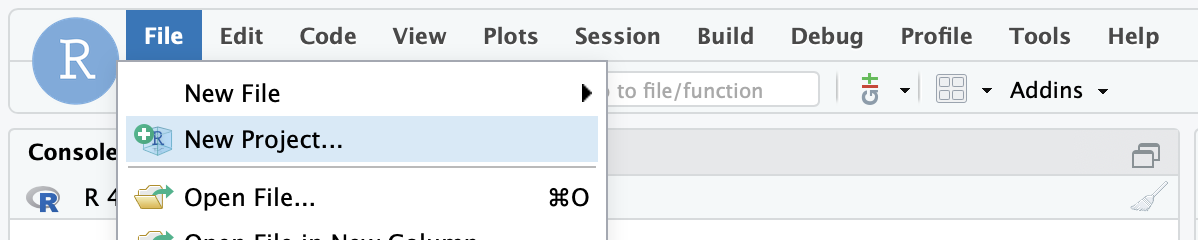
Step 2: Click “Version Control”

Click the third option.

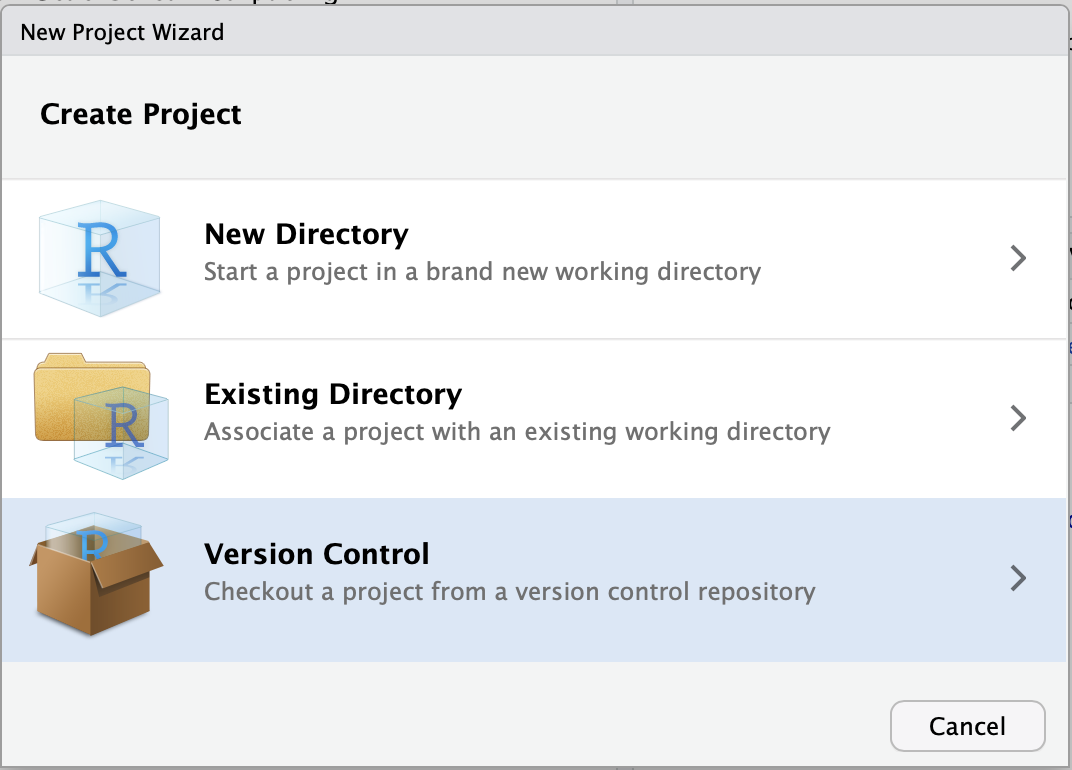
Step 3: Click Git

Click the first option

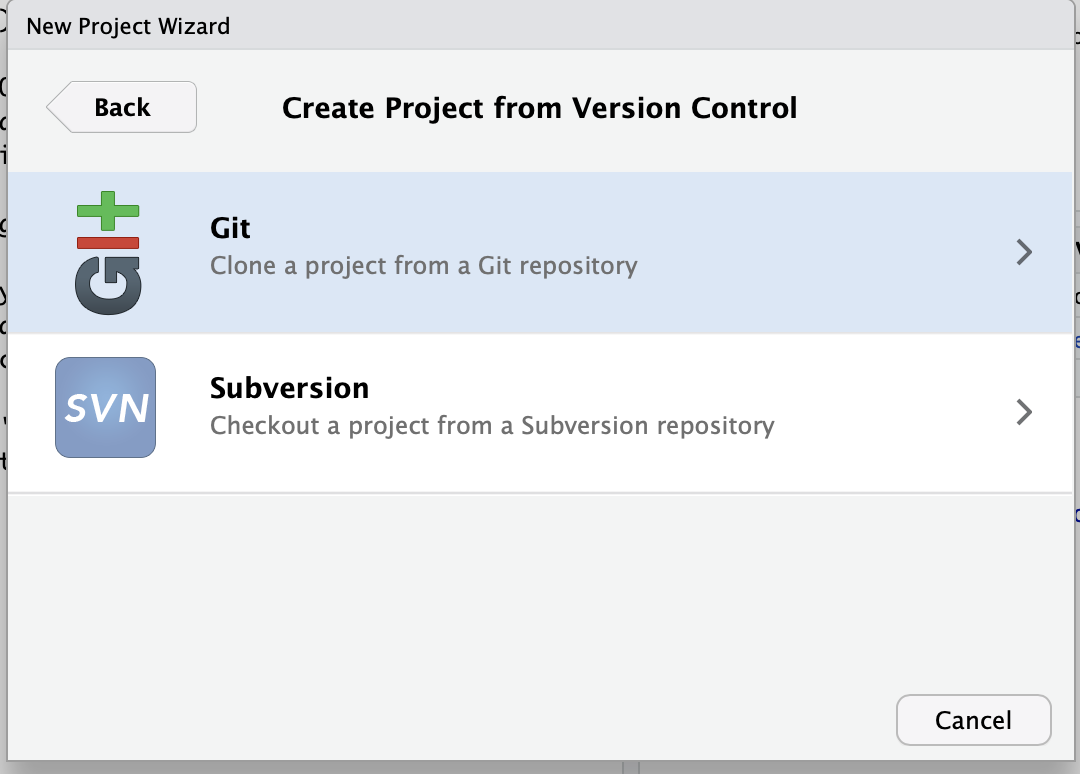
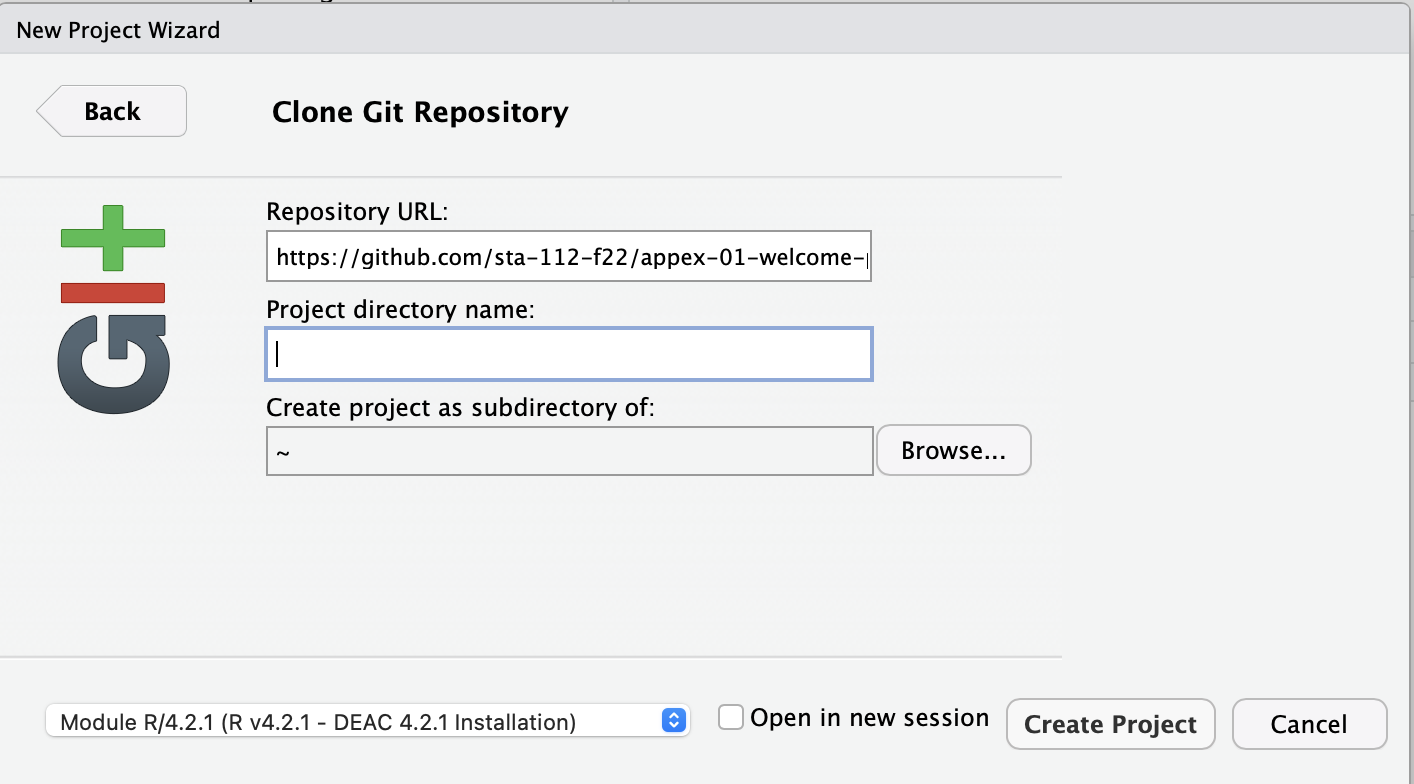
Step 4: Copy my starter files

Paste this link in the top box (Repository url):

https://github.com/sta-363-s23/06-appex.git

Part 1

1. Write a pipe that creates a model that uses lm() to fit a linear regression using tidymodels. Save it as lm_spec and look at the object. What does it return?

Part 2

1. Fit the model:

library(ISLR)
lm_fit <- fit(lm_spec,
              mpg ~ horsepower,
              data = Auto)
lm_fit

Does this give the same results as

lm(mpg ~ horsepower, data = Auto)

Part 3

1. Edit the code below to add the original data to the predicted data.

mpg_pred <- lm_fit |> 
  predict(new_data = Auto) |> 
  ---

Part 4

1. Copy the code below, fill in the blanks to fit a model on the training data then calculate the test RMSE.

set.seed(100)
Auto_split  <- ________
Auto_train  <- ________
Auto_test   <- ________
lm_fit      <- fit(lm_spec, 
                   mpg ~ horsepower, 
                   data = ________)
mpg_pred  <- ________ |> 
  predict(new_data = ________) |> 
  bind_cols(________)
rmse(________, truth = ________, estimate = ________)

Part 5

1. Edit the code below to get the 5-fold cross validation error rate for the following model:

\(mpg = \beta_0 + \beta_1 horsepower + \beta_2 horsepower^2+ \epsilon\)

Auto_cv <- vfold_cv(Auto, v = 5)

results <- fit_resamples(lm_spec,
                         ----,
                         resamples = ---)

results |>
  collect_metrics()

• What do you think rsq is?

Part 6

1. Fit 3 models on the data using 5 fold cross validation:

   \(mpg = \beta_0 + \beta_1 horsepower + \epsilon\)

   \(mpg = \beta_0 + \beta_1 horsepower + \beta_2 horsepower^2+ \epsilon\)

   \(mpg = \beta_0 + \beta_1 horsepower + \beta_2 horsepower^2+ \beta_3 horsepower^3 +\epsilon\)

2. Collect the metrics from each model, saving the results as results_1, results_2, results_3

3. Which model is “best”?