Appex 11 – Penalized Regression in R

STA 363 - Spring 2023

Set up

Login to RStudio Pro

Step 1: Create a New Project

Click File > New Project

Step 2: Click “Version Control”

Click the third option.

Step 3: Click Git

Click the first option

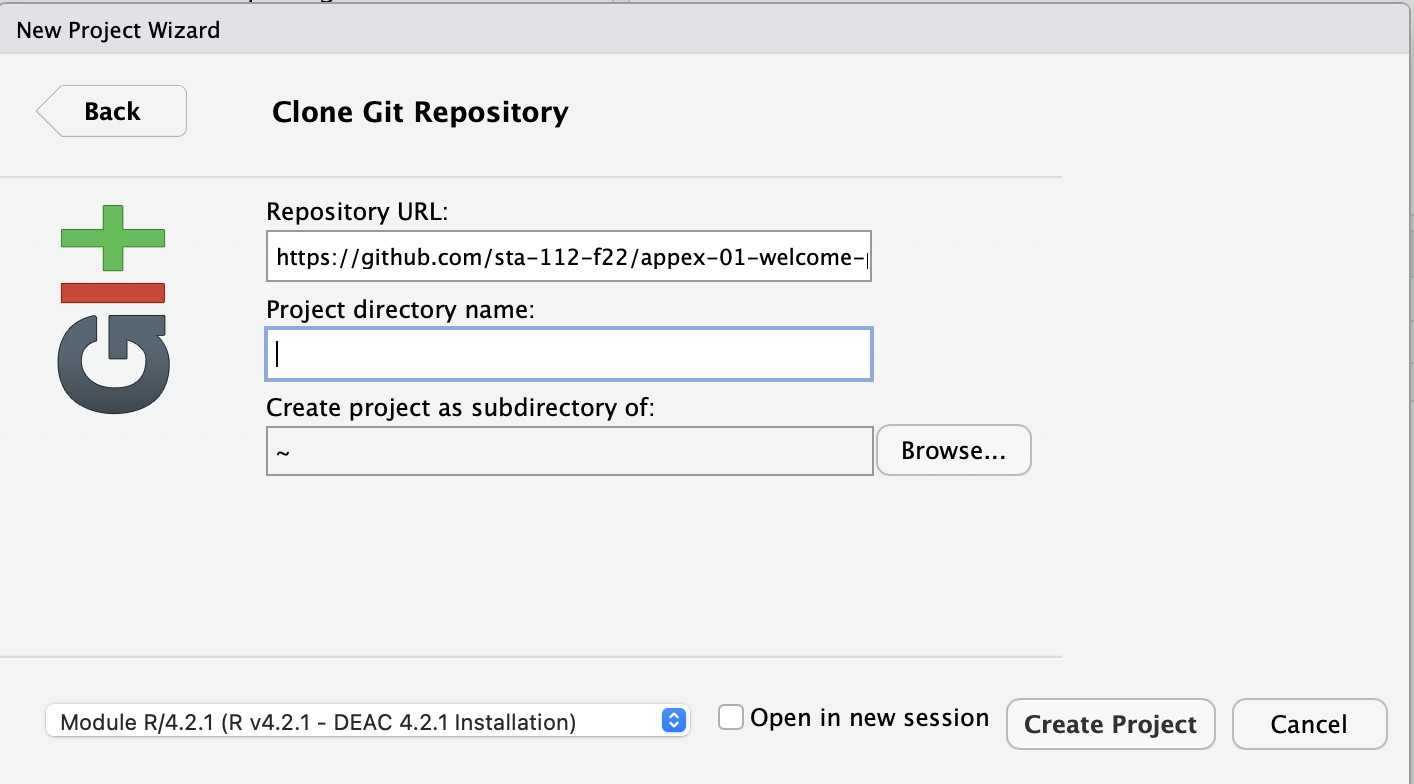
Step 4: Copy my starter files

Paste this link in the top box (Repository url):

https://github.com/sta-363-s23/11-appex.git

Part 1

  1. Examine the Hitters dataset by running ?Hitters in the Console
  2. We want to predict a major league player’s Salary from all of the other 19 variables in this dataset. Create a visualization of Salary.
  3. Create a recipe to estimate this model.
  4. Add a preprocessing step to your recipe, scaling each of the predictors

Part 2

  1. Add a preprocessing step to your recipe to convert nominal variables into indicators
  2. Add a step to your recipe to remove missing values for the outcome
  3. Add a step to your recipe to impute missing values for the predictors using the average for the remaining values NOTE THIS IS NOT THE BEST WAY TO DO THIS WE WILL LEARN BETTER TECHNIQUES!

Part 3

  1. Set a seed set.seed(1)
  2. Create a cross validation object for the Hitters dataset
  3. Using the recipe from the previous exercise, fit the model using Ridge regression with a penalty \(\lambda\) = 300
  4. What is the estimate of the test RMSE for this model?

Part 4

  1. Using the Hitters cross validation object and recipe created in the previous exercise, use tune_grid to pick the optimal penalty and mixture values.
  2. Update the code below to create a grid that includes penalties from 0 to 50 by 1 and mixtures from 0 to 1 by 0.5.
  3. Use this grid in the tune_grid function. Then use collect_metrics and filter to only include the RSME estimates.
  4. Create a figure to examine the estimated test RMSE for the grid of penalty and mixture values – which should you choose?

Part 5

  1. Using the final model specification, extract the coefficients from the model by creating a workflow
  2. Filter out any coefficients exactly equal to 0