Cross validation

Dr. D’Agostino McGowan

Cross validation

💡 Big idea

We have determined that it is sensible to use a test set to calculate metrics like prediction error

Cross validation

💡 Big idea

We have determined that it is sensible to use a test set to calculate metrics like prediction error

Why?

Cross validation

💡 Big idea

We have determined that it is sensible to use a test set to calculate metrics like prediction error

How could we do this?

Cross validation

💡 Big idea

We have determined that it is sensible to use a test set to calculate metrics like prediction error
What if we don’t have a separate data set to test our model on?
🎉 We can use resampling methods to estimate the test-set prediction error

Training error versus test error

What is the difference? Which is typically larger?

The training error is calculated by using the same observations used to fit the statistical learning model
The test error is calculated by using a statistical learning method to predict the response of new observations
The training error rate typically underestimates the true prediction error rate

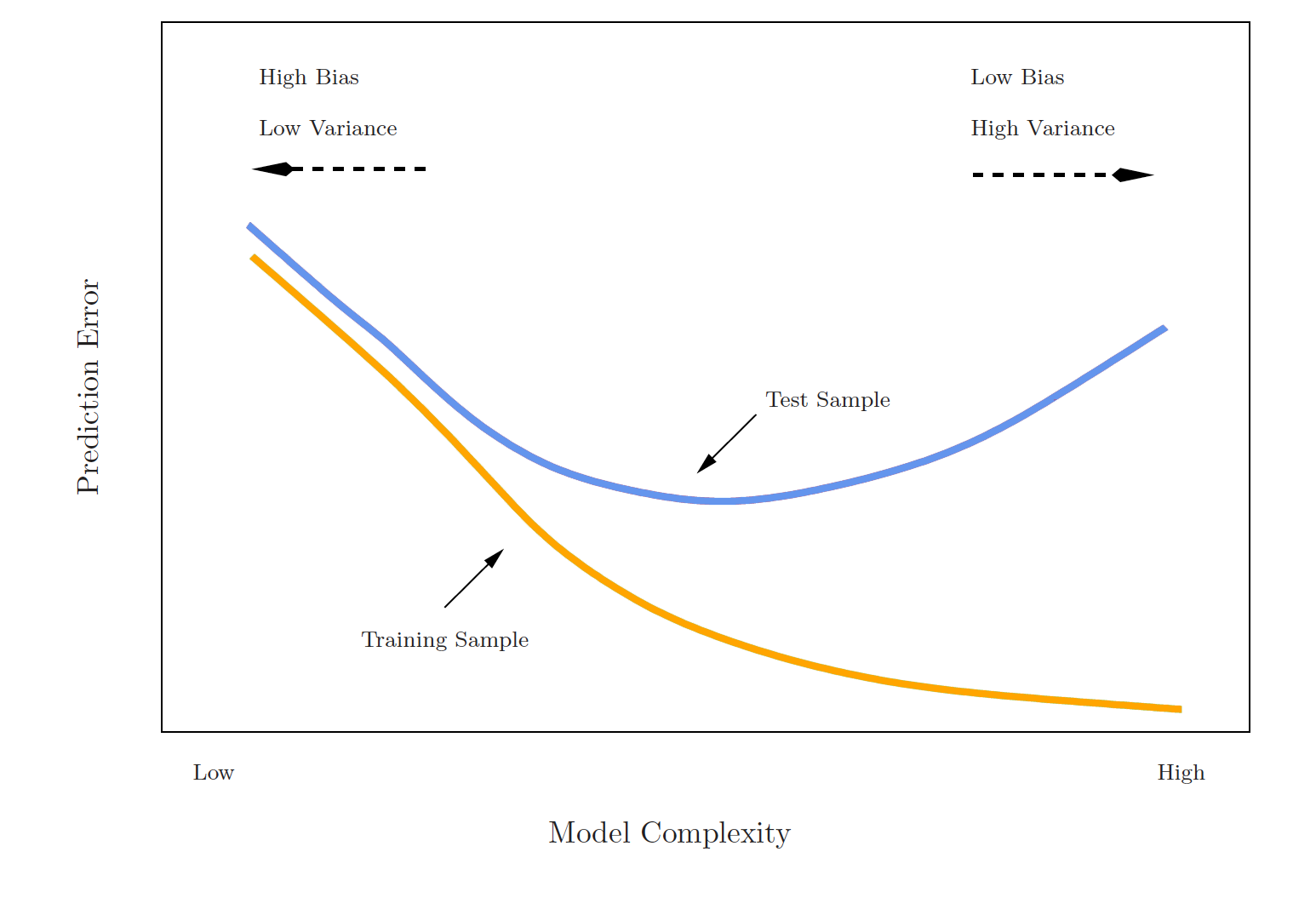
Estimating prediction error

Best case scenario: We have a large data set to test our model on
This is not always the case!

💡 Let’s instead find a way to estimate the test error by holding out a subset of the training observations from the model fitting process, and then applying the statistical learning method to those held out observations

Approach #1: Validation set

Randomly divide the available set up samples into two parts: a training set and a validation set
Fit the model on the training set, calculate the prediction error on the validation set

If we have a quantitative predictor what metric would we use to calculate this test error?

Often we use Mean Squared Error (MSE)

Approach #1: Validation set

Randomly divide the available set up samples into two parts: a training set and a validation set
Fit the model on the training set, calculate the prediction error on the validation set

If we have a qualitative predictor what metric would we use to calculate this test error?

Often we use misclassification rate

Approach #1: Validation set

\[\Large\color{orange}{MSE_{\texttt{test-split}} = \textrm{Ave}_{i\in\texttt{test-split}}[y_i-\hat{f}(x_i)]^2}\]

\[\Large\color{orange}{Err_{\texttt{test-split}} = \textrm{Ave}_{i\in\texttt{test-split}}I[y_i\neq \mathcal{\hat{C}}(x_i)]}\]

Approach #1: Validation set

Auto example:

We have 392 observations.
Trying to predict mpg from horsepower.
We can split the data in half and use 196 to fit the model and 196 to test

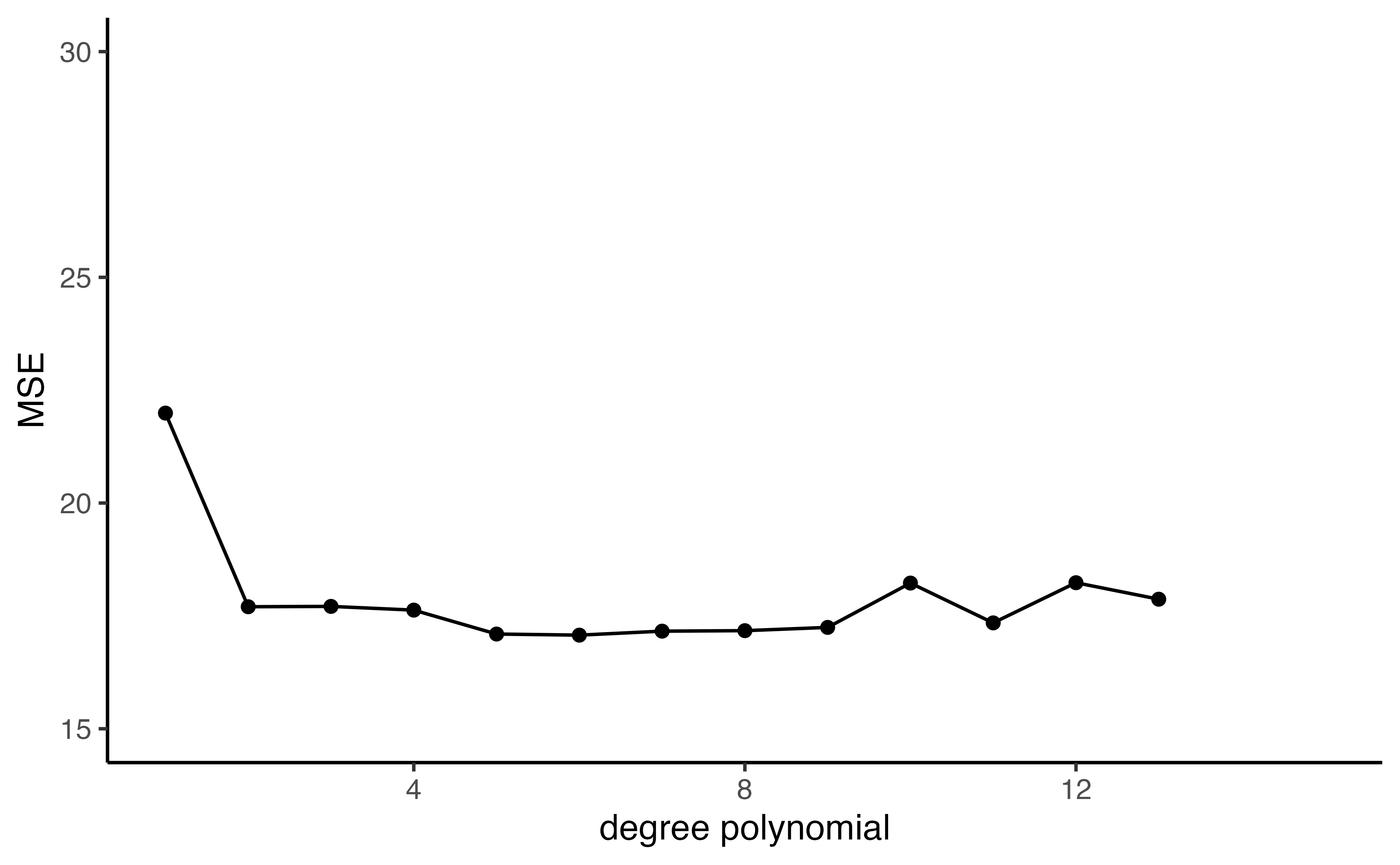
Approach #1: Validation set

\(\color{orange}{MSE_{\texttt{test-split}}}\)

\(\color{orange}{MSE_{\texttt{test-split}}}\)

\(\color{orange}{MSE_{\texttt{test-split}}}\)

\(\color{orange}{MSE_{\texttt{test-split}}}\)

Approach #1: Validation set

Auto example:

We have 392 observations.
Trying to predict mpg from horsepower.
We can split the data in half and use 196 to fit the model and 196 to test - what if we did this many times?

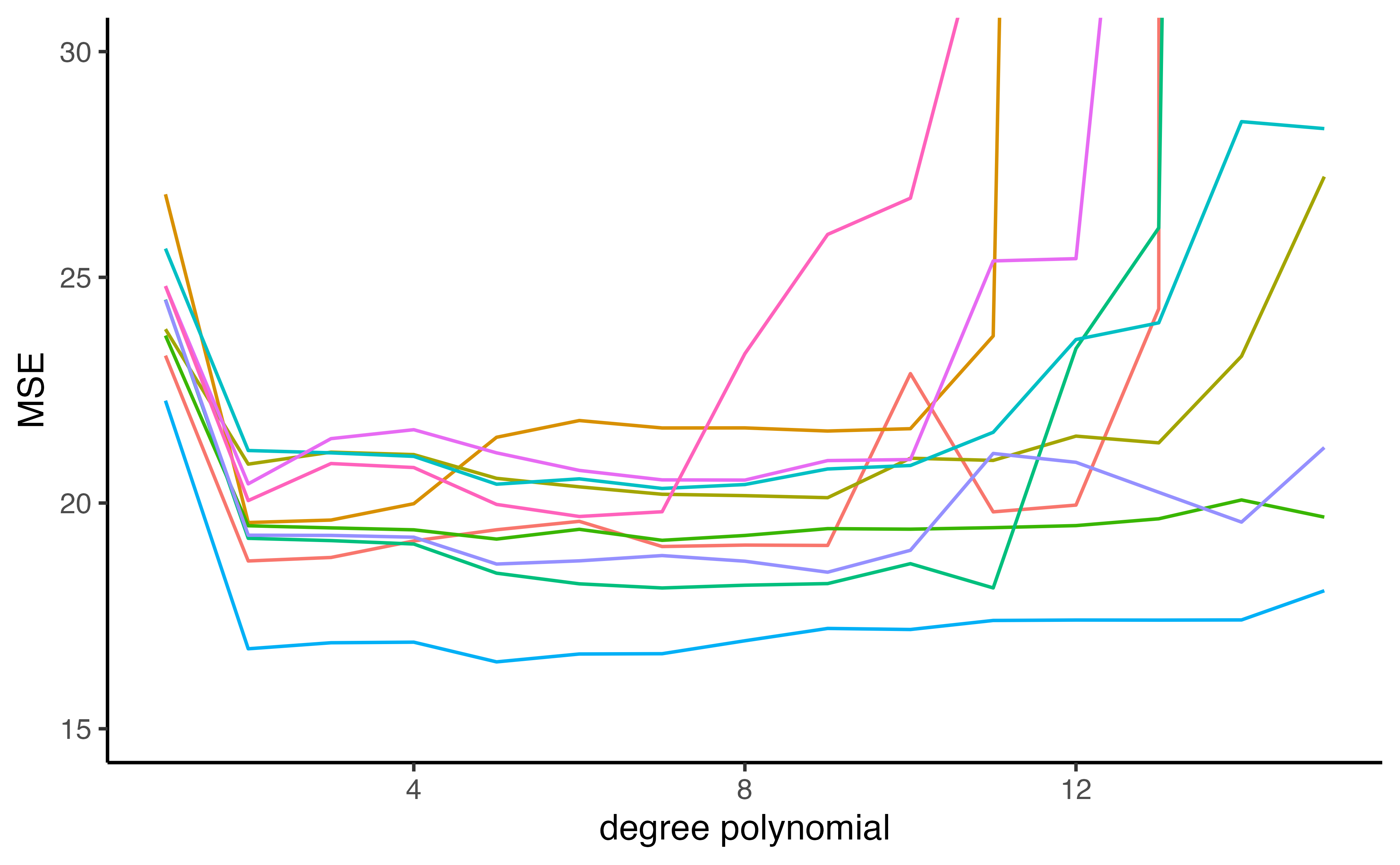
Approach #1: Validation set (Drawbacks)

the validation estimate of the test error can be highly variable, depending on which observations are included in the training set and which observations are included in the validation set
In the validation approach, only a subset of the observations (those that are included in the training set rather than in the validation set) are used to fit the model
Therefore, the validation set error may tend to overestimate the test error for the model fit on the entire data set

Approach #2: K-fold cross validation

💡 The idea is to do the following:

Randomly divide the data into \(K\) equal-sized parts
Leave out part \(k\), fit the model to the other \(K - 1\) parts (combined)
Obtain predictions for the left-out \(k\)th part
Do this for each part \(k = 1, 2,\dots K\), and then combine the result

K-fold cross validation

\(\color{orange}{MSE_{\texttt{test-split-1}}}\)

\(\color{orange}{MSE_{\texttt{test-split-2}}}\)

\(\color{orange}{MSE_{\texttt{test-split-3}}}\)

\(\color{orange}{MSE_{\texttt{test-split-4}}}\)

Take the mean of the \(k\) MSE values

`Application Exercise`

If we use 10 folds:

What percentage of the training data is used in each analysis for each fold?
What percentage of the training data is used in the assessment for each fold?

02:00

Estimating prediction error (quantitative outcome)

Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
\(CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k\)
\(MSE_k = \sum_{i \in C_k} (y_i - \hat{y}_i)^2/n_k\)
\(n_k\) is the number of observations in group \(k\)
\(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed
If we set \(K = n\), we’d have \(n-fold\) cross validation which is the same as leave-one-out cross validation (LOOCV)

Estimating prediction error (quantitative outcome)

Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
\[CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k\]
\(MSE_k = \sum_{i \in C_k} (y_i - \hat{y}_i)^2/n_k\)
\(n_k\) is the number of observations in group \(k\)
\(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed
If we set \(K = n\), we’d have \(n-fold\) cross validation which is the same as leave-one-out cross validation (LOOCV)

Leave-one-out cross validation

\[\dots\]

Special Case!

With linear regression, you can actually calculate the LOOCV error without having to iterate!
\(CV_{(n)} = \frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{y}_i}{1-h_i}\right)^2\)
\(\hat{y}_i\) is the \(i\)th fitted value from the linear model
\(h_i\) is the diagonal of the “hat” matrix (remember that! 🎓)

Picking \(K\)

\(K\) can vary from 2 (splitting the data in half each time) to \(n\) (LOOCV)
LOOCV is sometimes useful but usually the estimates from each fold are very correlated, so their average can have a high variance
A better choice tends to be \(K=5\) or \(K=10\)

Bias variance trade-off

Since each training set is only \((K - 1)/K\) as big as the original training set, the estimates of prediction error will typically be biased upward
This bias is minimized when \(K = n\) (LOOCV), but this estimate has a high variance
\(K =5\) or \(K=10\) provides a nice compromise for the bias-variance trade-off

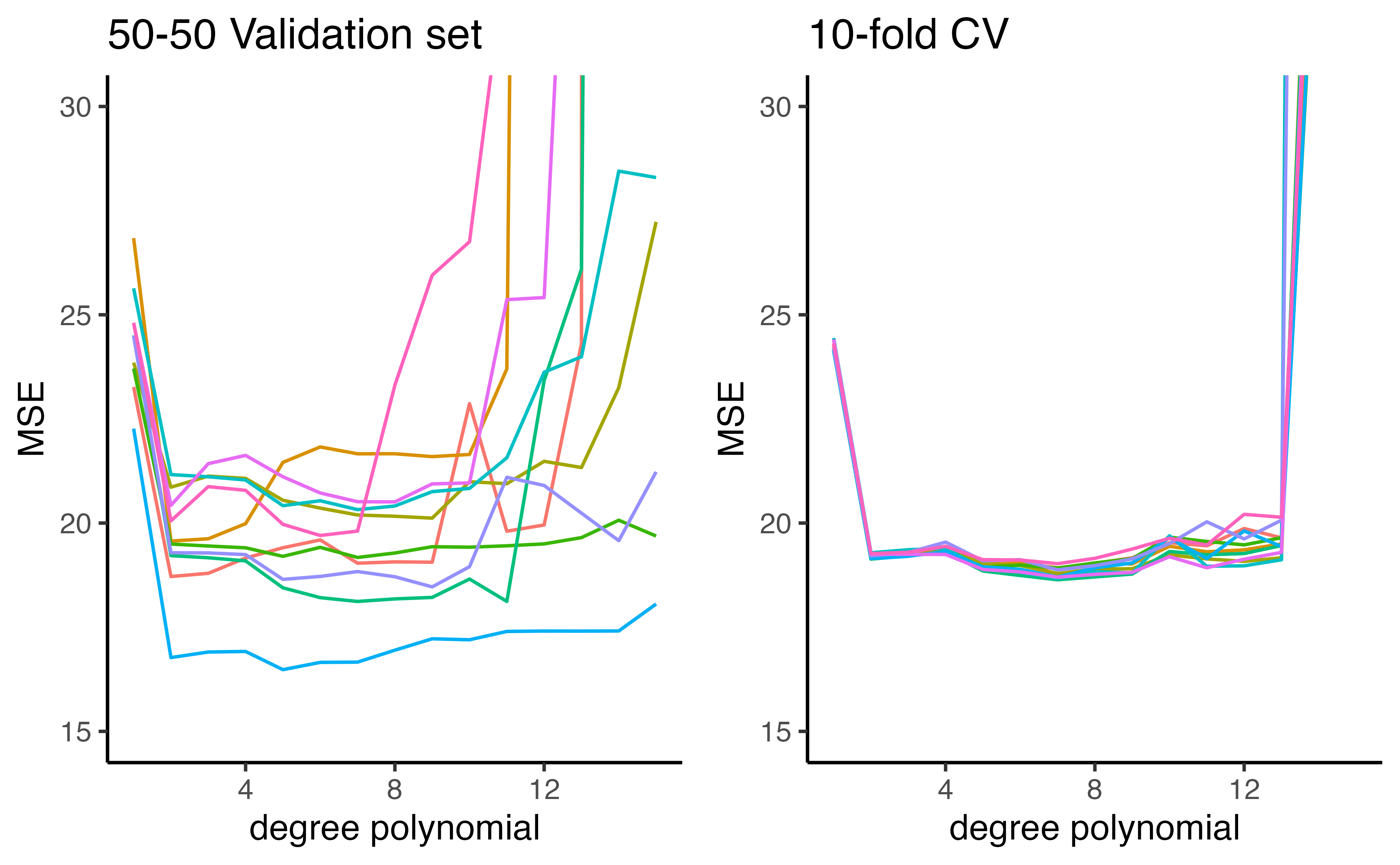
Approach #2: K-fold Cross Validation

Auto example:

We have 392 observations.
Trying to predict mpg from horsepower

Estimating prediction error (qualitative outcome)

The premise is the same as cross valiation for quantitative outcomes
Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
\(CV_K = \sum_{k=1}^K\frac{n_k}{n}Err_k\)
\(Err_k = \sum_{i\in C_k}I(y_i\neq\hat{y}_i)/n_k\) (misclassification rate)
\(n_k\) is the number of observations in group \(k\)
\(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed

Estimating prediction error (qualitative outcome)

The premise is the same as cross valiation for quantitative outcomes
Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
\(CV_K = \sum_{k=1}^K\frac{n_k}{n}Err_k\)
\(Err_k = \sum_{i\in C_k}I(y_i\neq\hat{y}_i)/n_k\) (misclassification rate)
\(n_k\) is the number of observations in group \(k\)
\(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed