Linear Regression in R

Lucy D’Agostino McGowan

Application Exercise

  1. Create a new project from this template in RStudio Pro:
https://github.com/sta-363-s23/08-appex.git
  1. Load the packages and data by running the top chunk of R code

Let’s look at an example

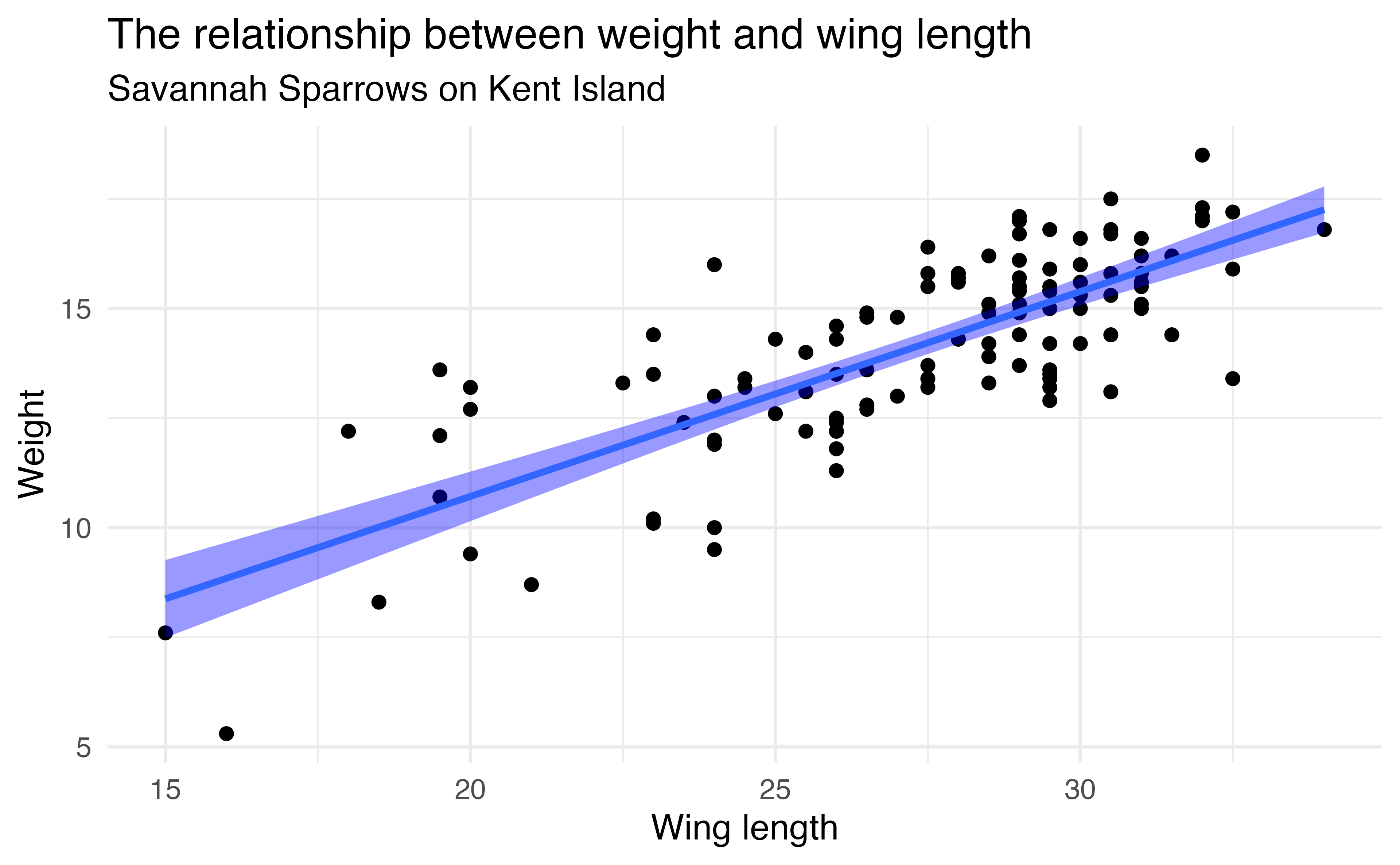
Let’s look at a sample of 116 sparrows from Kent Island. We are interested in the relationship between Weight and Wing Length

  • the standard error of \(\hat{\beta_1}\) ( \(SE_{\hat{\beta}_1}\) ) is how much we expect the sample slope to vary from one random sample to another.

Sparrows

How can we quantify how much we’d expect the slope to differ from one random sample to another?

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1
2 WingLength     0.467    0.0347     13.5  2.62e-25

Sparrows

How can we quantify how much we’d expect the slope to differ from one random sample to another?

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1
2 WingLength     0.467    0.0347     13.5  2.62e-25

Sparrows

How do we interpret this?

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1
2 WingLength     0.467    0.0347     13.5  2.62e-25
  • “the sample slope is more than 13 standard errors above a slope of zero”

Sparrows

How do we know what values of this statistic are worth paying attention to?

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy(conf.int = TRUE)
# A tibble: 2 × 7
  term        estimate std.error statistic  p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1   -0.531     3.26 
2 WingLength     0.467    0.0347     13.5  2.62e-25    0.399     0.536
  • confidence intervals
  • p-values

Application Exercise

  1. Fit a linear model using the mtcars data frame predicting miles per gallon (mpg) from weight and horsepower (wt and hp).
  2. Pull out the coefficients and confidence intervals using the tidy() function demonstrated. How do you interpret these?
04:00

Sparrows

How are these statistics distributed under the null hypothesis?

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy() 
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1
2 WingLength     0.467    0.0347     13.5  2.62e-25

Sparrows

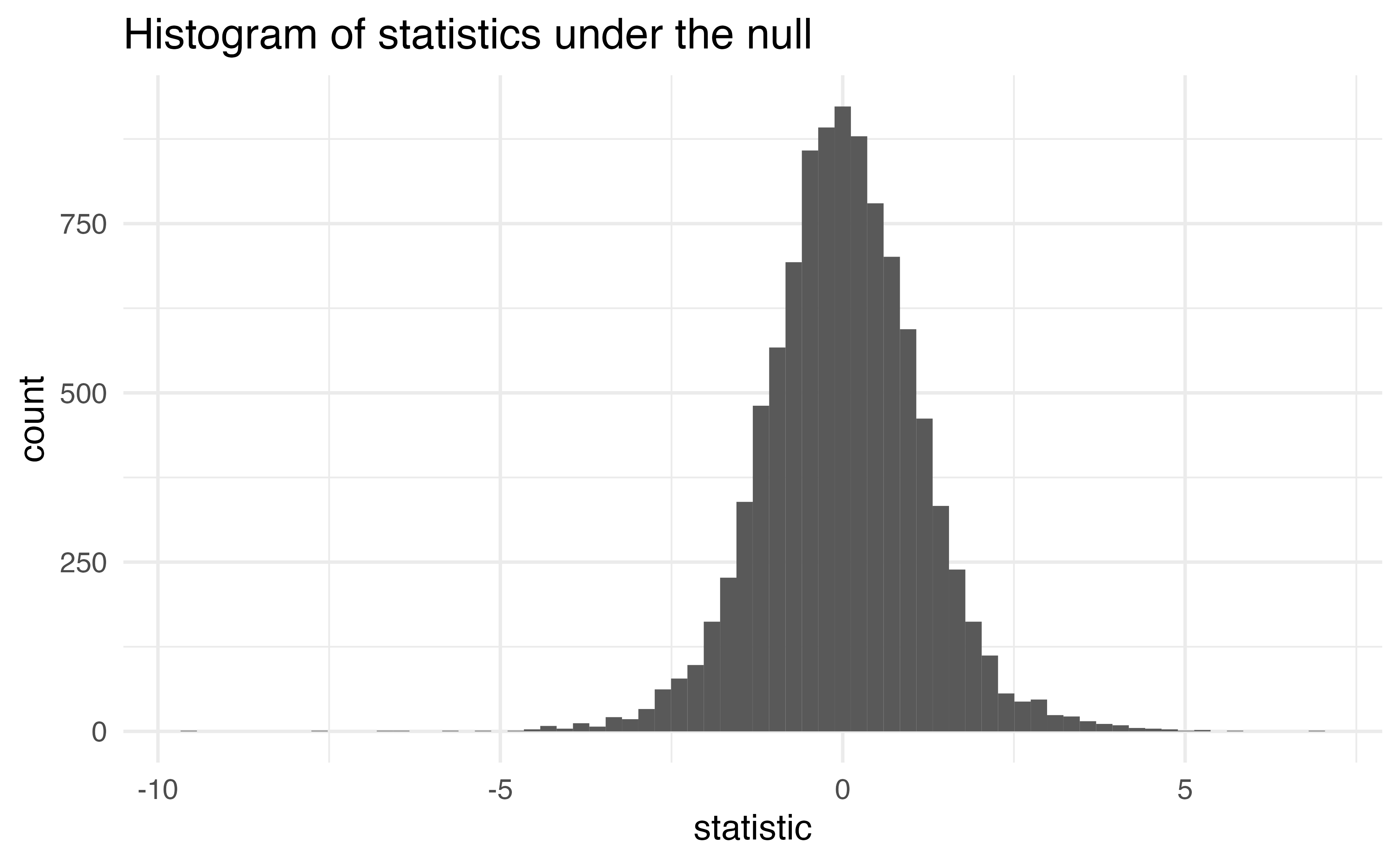
  • I’ve generated some data under a null hypothesis where \(n = 20\)

Sparrows

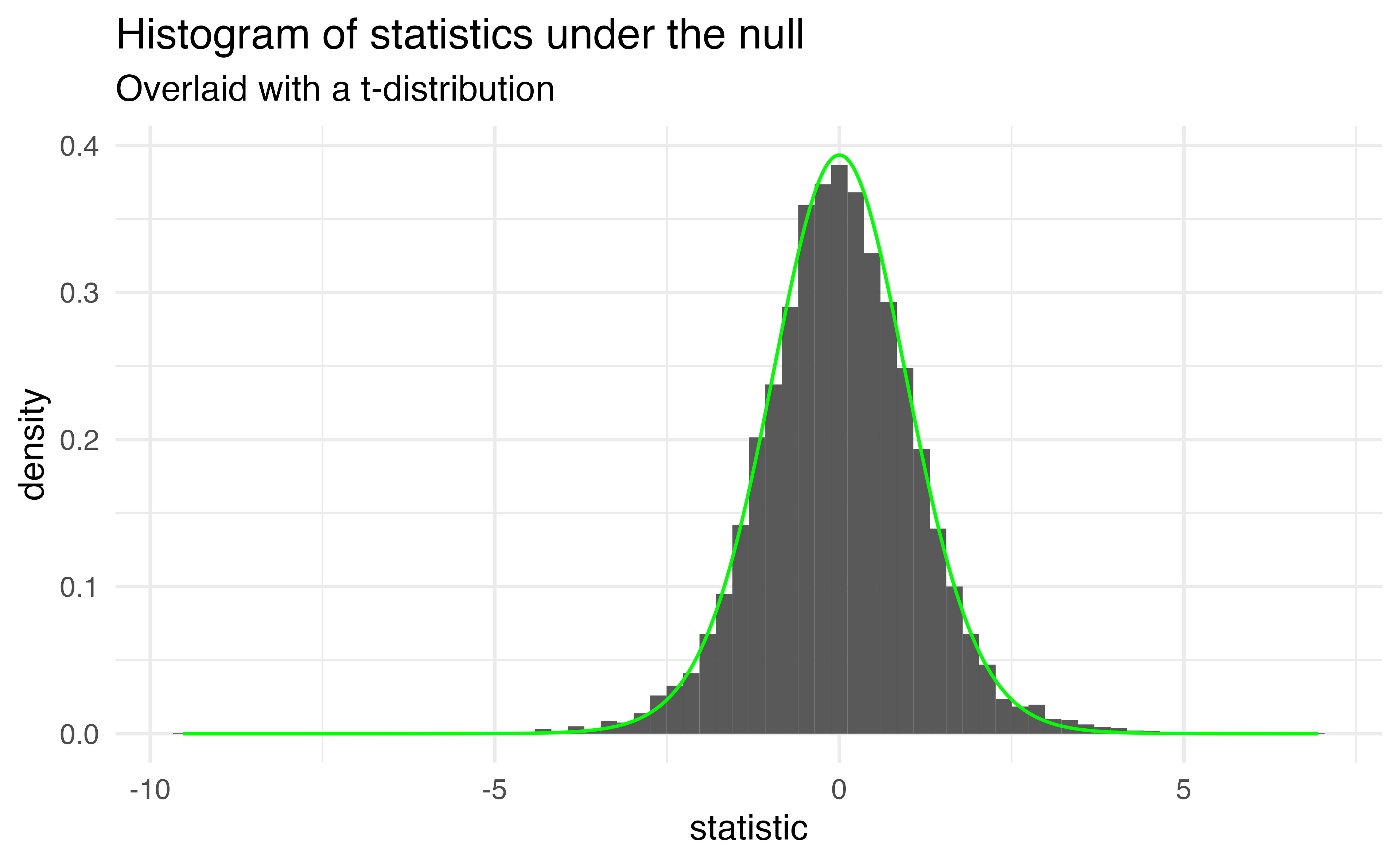
  • this is a t-distribution with n-p-1 degrees of freedom.

Sparrows

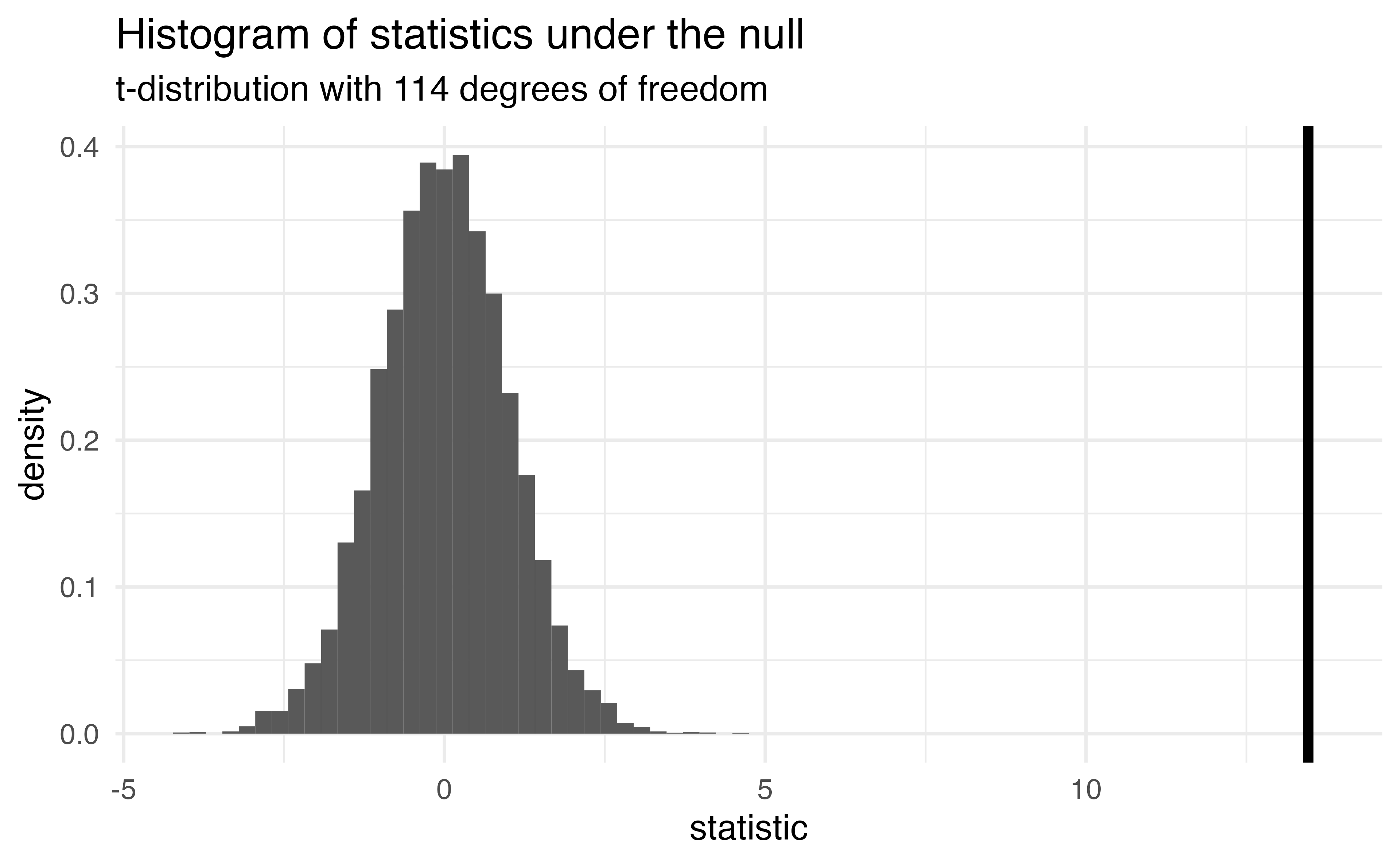
The distribution of test statistics we would expect given the null hypothesis is true, \(\beta_1 = 0\), is t-distribution with n-2 degrees of freedom.

Sparrows

Sparrows

How can we compare this line to the distribution under the null?

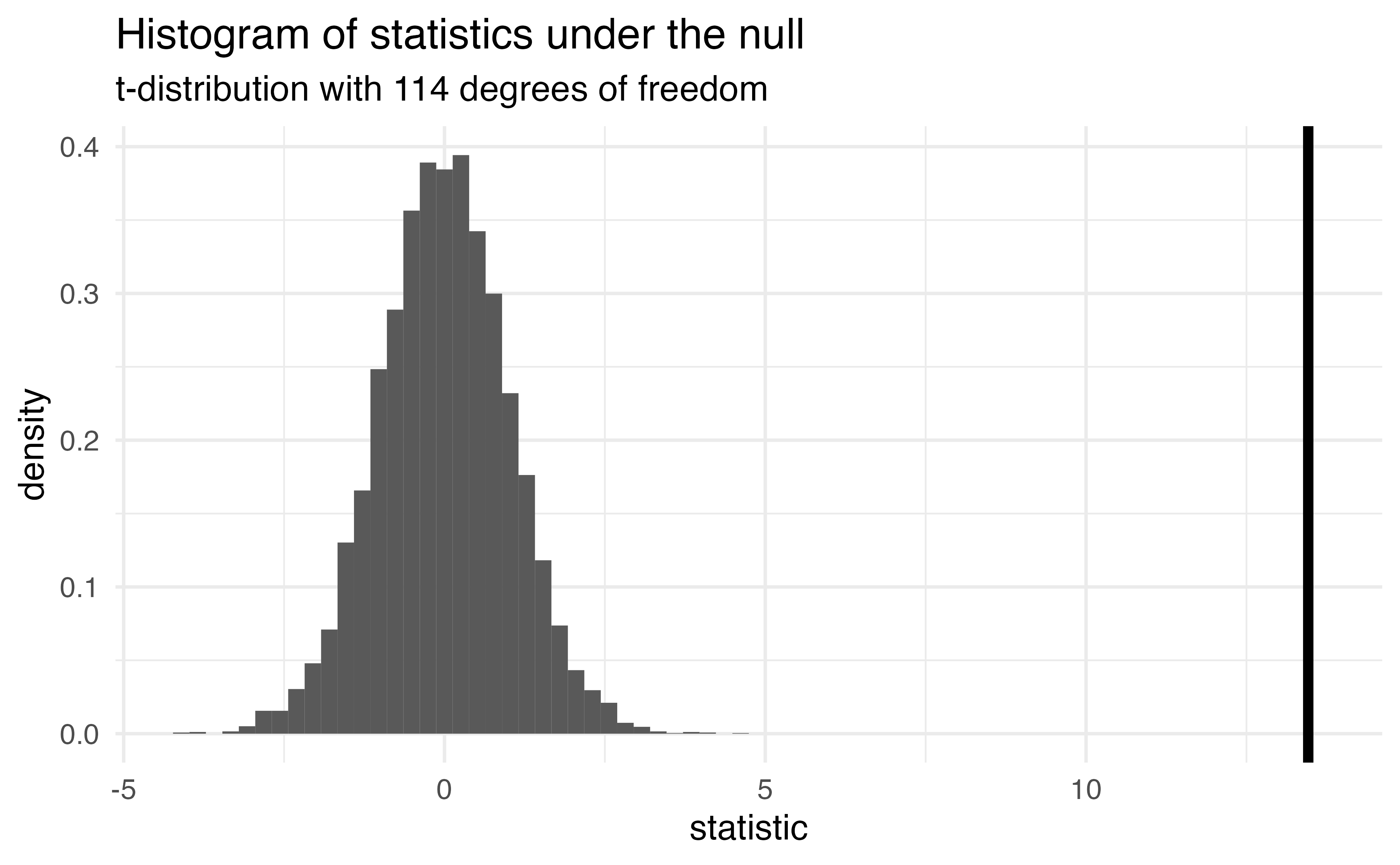
  • p-value

p-value

The probability of getting a statistic as extreme or more extreme than the observed test statistic given the null hypothesis is true

Sparrows

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1
2 WingLength     0.467    0.0347     13.5  2.62e-25

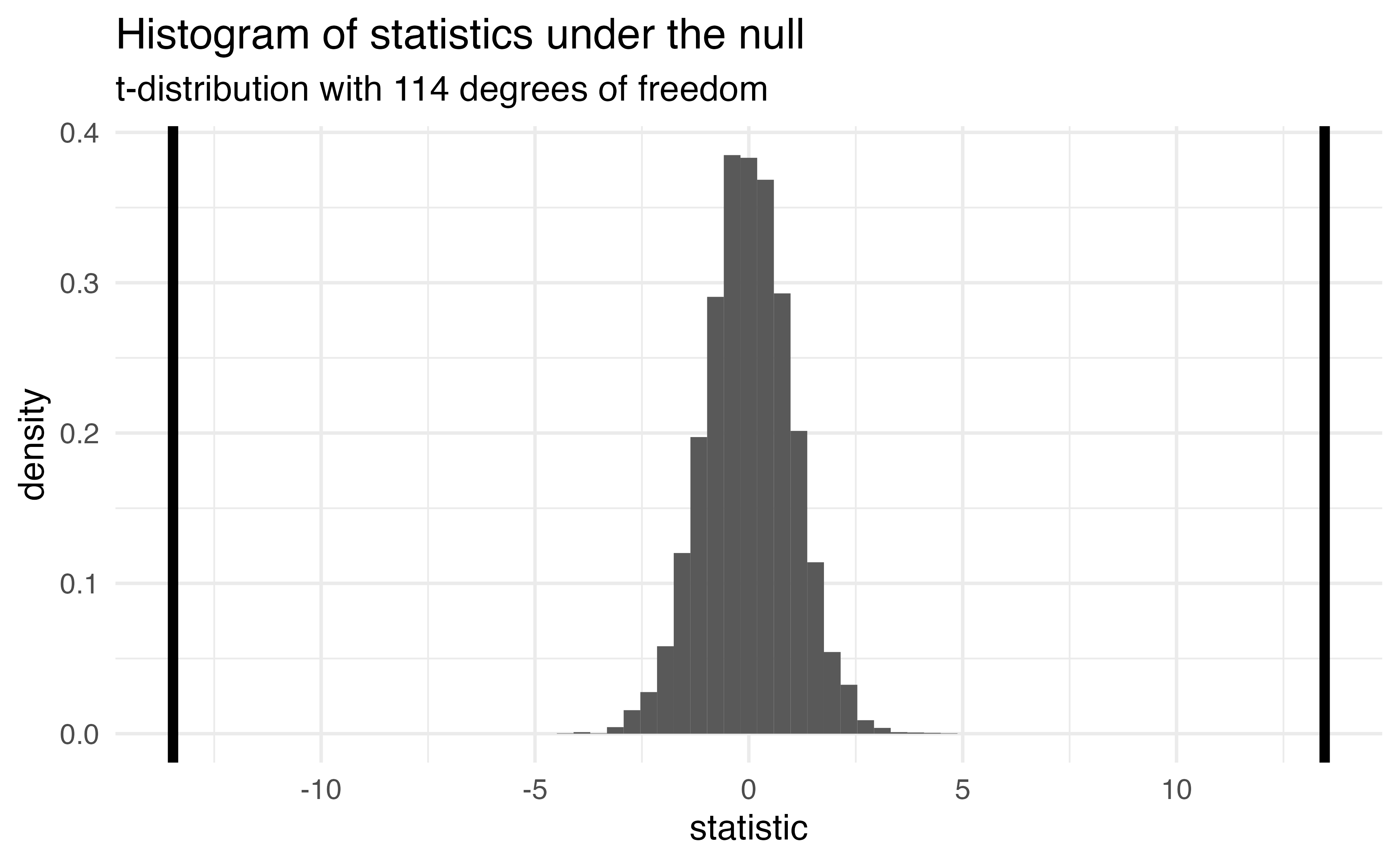
Return to generated data, n = 20

  • Let’s say we get a statistic of 1.5 in a sample

Let’s do it in R!

The proportion of area less than 1.5

pt(1.5, df = 18)
[1] 0.9245248

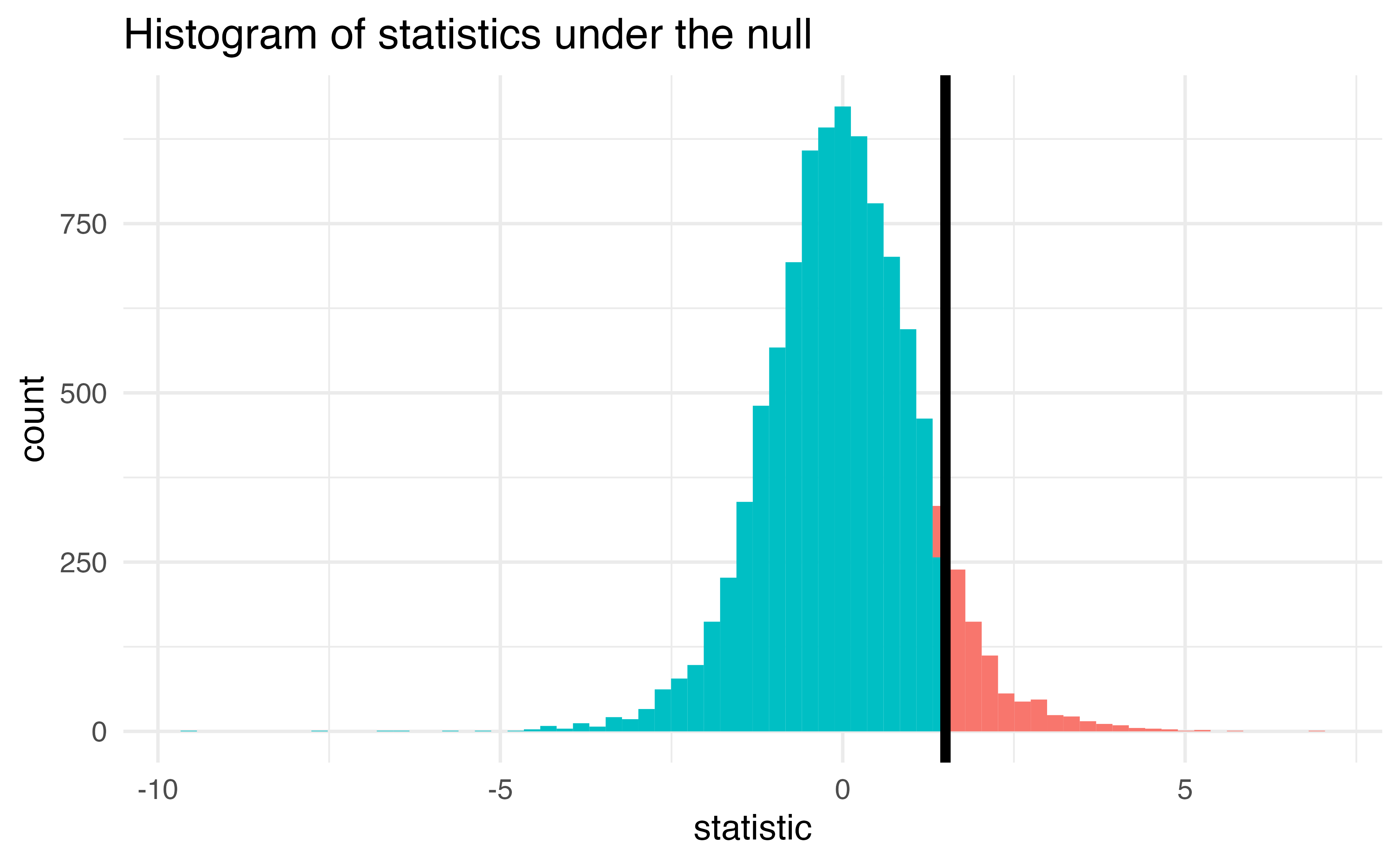
Let’s do it in R!

The proportion of area greater than 1.5

pt(1.5, df = 18, lower.tail = FALSE)
[1] 0.07547523

Let’s do it in R!

The proportion of area greater than 1.5 or less than -1.5.

pt(1.5, df = 18, lower.tail = FALSE) * 2
[1] 0.1509505

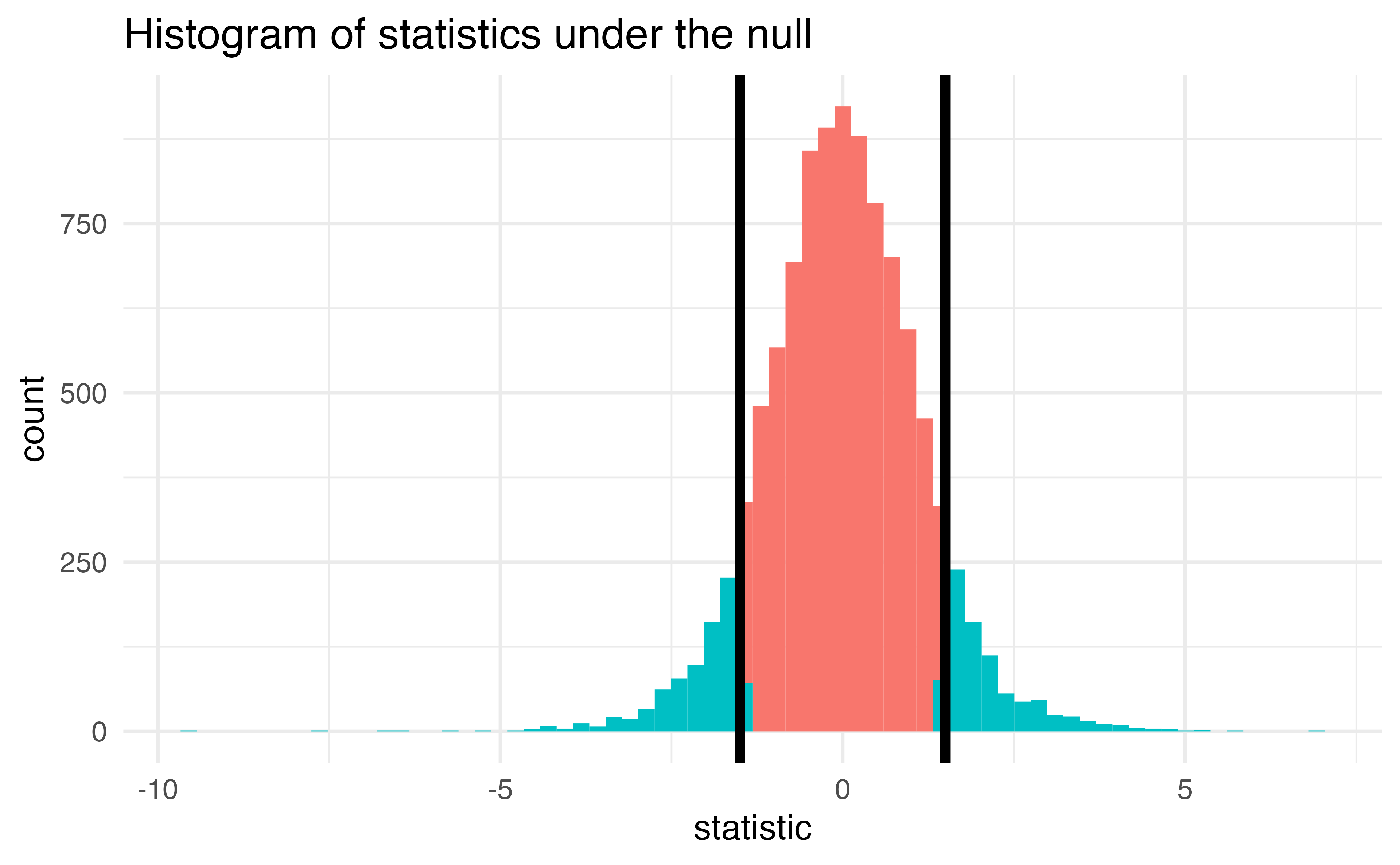
p-value

The probability of getting a statistic as extreme or more extreme than the observed test statistic given the null hypothesis is true

Hypothesis test

  • null hypothesis \(H_0: \beta_1 = 0\)
  • alternative hypothesis \(H_A: \beta_1 \ne 0\)
  • p-value: 0.15
  • Often, we have an \(\alpha\)-level cutoff to compare this to, for example 0.05. Since this is greater than 0.05, we fail to reject the null hypothesis

Application Exercise

  1. Using the linear model you fit previously (mpg from wt and hp) - calculate the p-value for the coefficient for weight
  2. Interpret this value. What is the null hypothesis? What is the alternative hypothesis? Do you reject the null?
04:00

confidence intervals

If we use the same sampling method to select different samples and computed an interval estimate for each sample, we would expect the true population parameter ( \(\beta_1\) ) to fall within the interval estimates 95% of the time.

Confidence interval

\[\Huge \hat\beta_1 \pm t^∗ \times SE_{\hat\beta_1}\]

  • \(t^*\) is the critical value for the \(t_{n−p-1}\) density curve to obtain the desired confidence level
  • Often we want a 95% confidence level.

Let’s do it in R!

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy(conf.int = TRUE)
# A tibble: 2 × 7
  term        estimate std.error statistic  p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1   -0.531     3.26 
2 WingLength     0.467    0.0347     13.5  2.62e-25    0.399     0.536
  • \(t^* = t_{n-p-1} = t_{114} = 1.98\)
  • \(LB = 0.47 - 1.98\times 0.0347 = 0.399\)
  • \(UB = 0.47+1.98 \times 0.0347 = 0.536\)

confidence intervals

If we use the same sampling method to select different samples and computed an interval estimate for each sample, we would expect the true population parameter ( \(\beta_1\) ) to fall within the interval estimates 95% of the time.

Linear Regression Questions

  • ✔️ Is there a relationship between a response variable and predictors?
  • ✔️ How strong is the relationship?
  • ✔️ What is the uncertainty?
  • How accurately can we predict a future outcome?

Sparrows

Using the information here, how could I predict a new sparrow’s weight if I knew the wing length was 30?

linear_reg() |>
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows) |>
  tidy()
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    1.37     0.957       1.43 1.56e- 1
2 WingLength     0.467    0.0347     13.5  2.62e-25
  • \(1.37 + 0.467 \times 30 = 15.38\)

Linear Regression Accuracy

What is the residual sum of squares again?

  • Note: In previous classes, this may have been referred to as SSE (sum of squares error), the book uses RSS, so we will stick with that!

\[RSS = \sum(y_i - \hat{y}_i)^2\]

Linear Regression Accuracy

  • The total sum of squares represents the variability of the outcome, it is equivalent to the variability described by the model plus the remaining residual sum of squares

\[TSS = \sum(y_i - \bar{y})^2\]

Linear Regression Accuracy

  • There are many ways “model fit” can be assessed. Two common ones are:
    • Residual Standard Error (RSE)
    • \(R^2\) - the fraction of the variance explained
  • \(RSE = \sqrt{\frac{1}{n-p-1}RSS}\)
  • \(R^2 = 1 - \frac{RSS}{TSS}\)

Let’s do it in R!

lm_fit <- linear_reg() |> 
  set_engine("lm") |>
  fit(Weight ~ WingLength, data = Sparrows)

lm_fit |>
  predict(new_data = Sparrows) |>
  bind_cols(Sparrows) |>
  rsq(truth = Weight, estimate = .pred) 
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rsq     standard       0.614

Is this testing \(R^2\) or training \(R^2\)?

Application Exercise

  1. Fit a linear model using the mtcars data frame predicting miles per gallon (mpg) from weight and horsepower (wt and hp), using polynomials with 4 degrees of freedom for both.
  2. Estimate the training \(R^2\) using the rsq function.
  3. Interpret this values.
04:00

Application Exercise

  1. Create a cross validation object to do 5 fold cross validation using the mtcars data
  2. Refit the model on this object (using fit_resamples)
  3. Use collect_metrics to estimate the test \(R^2\) - how does this compare to the training \(R^2\) calculated in the previous exercise?
04:00

Additional Linear Regression Topics

  • Polynomial terms
  • Interactions
  • Outliers
  • Non-constant variance of error terms
  • High leverage points
  • Collinearity

Refer to Chapter 3 for more details on these topics if you need a refresher.

Dr. Lucy D’Agostino McGowan