tidymodels

Application Exercise

  1. Create a new project from this template in RStudio Pro:
https://github.com/sta-363-s23/11-appex.git
  1. Load the packages and data by running the top chunk of R code
02:00

tidymodels

lm_spec <- 
  linear_reg() |> # Pick linear regression
  set_engine(engine = "lm") # set engine
lm_spec
Linear Regression Model Specification (regression)

Computational engine: lm 
lm_fit <- fit(lm_spec,
              mpg ~ horsepower,
              data = Auto)

Validation set approach

Auto_split <- initial_split(Auto, prop = 0.5)
Auto_split
<Training/Testing/Total>
<196/196/392>

Extract the training and testing data

training(Auto_split)
testing(Auto_split)

A faster way!

  • You can use last_fit() and specify the split
  • This will automatically train the data on the train data from the split
  • Instead of specifying which metric to calculate (with rmse as before) you can just use collect_metrics() and it will automatically calculate the metrics on the test data from the split

A faster way!

set.seed(100)

Auto_split <- initial_split(Auto, prop = 0.5)
lm_fit <- last_fit(lm_spec,
                   mpg ~ horsepower,
                   split = Auto_split) 

lm_fit |>
  collect_metrics() 
# A tibble: 2 × 4
  .metric .estimator .estimate .config             
  <chr>   <chr>          <dbl> <chr>               
1 rmse    standard       4.96  Preprocessor1_Model1
2 rsq     standard       0.613 Preprocessor1_Model1

What about cross validation?

Auto_cv <- vfold_cv(Auto, v = 5)
Auto_cv
#  5-fold cross-validation 
# A tibble: 5 × 2
  splits           id   
  <list>           <chr>
1 <split [313/79]> Fold1
2 <split [313/79]> Fold2
3 <split [314/78]> Fold3
4 <split [314/78]> Fold4
5 <split [314/78]> Fold5

What if we wanted to do some preprocessing

  • For the shrinkage methods we discussed it was important to scale the variables

What does this mean?

What would happen if we scale before doing cross-validation? Will we get different answers?

What if we wanted to do some preprocessing

Auto_scaled <- Auto |>
  mutate(horsepower = scale(horsepower))

sd(Auto_scaled$horsepower)
[1] 1
Auto_cv_scaled <- vfold_cv(Auto_scaled, v = 5)

map_dbl(Auto_cv_scaled$splits,
        function(x) {
          dat <- as.data.frame(x)$horsepower
          sd(dat)
        })
[1] 1.0244697 1.0261352 0.9662367 0.9832638 0.9969558

What if we wanted to do some preprocessing

  • recipe()!
  • Using the recipe() function along with step_*() functions, we can specify preprocessing steps and R will automagically apply them to each fold appropriately.
rec <- recipe(mpg ~ horsepower, data = Auto) |>
  step_scale(horsepower)
  • You can find all of the potential preprocessing steps here: https://tidymodels.github.io/recipes/reference/index.html

Where do we plug in this recipe?

  • The recipe gets plugged into the fit_resamples() function
Auto_cv <- vfold_cv(Auto, v = 5)

rec <- recipe(mpg ~ horsepower, data = Auto) |>
  step_scale(horsepower)

results <- fit_resamples(lm_spec,
                         preprocessor = rec,
                         resamples = Auto_cv)

results |>
  collect_metrics()
# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   4.91      5  0.233  Preprocessor1_Model1
2 rsq     standard   0.615     5  0.0313 Preprocessor1_Model1

What if we want to predict mpg with more variables

  • Now we still want to add a step to scale predictors
  • We could either write out all predictors individually to scale them
  • OR we could use the all_predictors() short hand.
rec <- recipe(mpg ~ horsepower + displacement + weight, data = Auto) |>
  step_scale(all_predictors())

Putting it together

rec <- recipe(mpg ~ horsepower + displacement + weight, data = Auto) |>
  step_scale(all_predictors())

results <- fit_resamples(lm_spec,
                         preprocessor = rec,
                         resamples = Auto_cv)

results |>
  collect_metrics()
# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   4.24      5  0.206  Preprocessor1_Model1
2 rsq     standard   0.711     5  0.0148 Preprocessor1_Model1

Application Exercise

  1. Examine the Hitters dataset by running ?Hitters in the Console
  2. We want to predict a major league player’s Salary from all of the other 19 variables in this dataset. Create a visualization of Salary.
  3. Create a recipe to estimate this model.
  4. Add a preprocessing step to your recipe, scaling each of the predictors
06:00

What if we have categorical variables?

  • We can turn the categorical variables into indicator (“dummy”) variables in the recipe
rec <- recipe(mpg ~ horsepower + displacement + weight, data = Auto) |>
  step_dummy(all_nominal()) |>
  step_scale(all_predictors())

What if we have missing data?

  • We can remove any rows with missing data
rec <- recipe(mpg ~ horsepower + displacement + weight, data = Auto) |>
  step_dummy(all_nominal()) |>
  step_naomit(everything()) |>
  step_scale(all_predictors())

What if we have missing data?

rec <- recipe(mpg ~ horsepower + displacement + weight, data = Auto) |>
  step_dummy(all_nominal()) |>
  step_naomit(all_outcomes()) |>
  step_impute_mean(all_predictors()) |>
  step_scale(all_predictors())

Application Exercise

  1. Add a preprocessing step to your recipe to convert nominal variables into indicators
  2. Add a step to your recipe to remove missing values for the outcome
  3. Add a step to your recipe to impute missing values for the predictors using the average for the remaining values NOTE THIS IS NOT THE BEST WAY TO DO THIS WE WILL LEARN BETTER TECHNIQUES!
06:00

Ridge, Lasso, and Elastic net

When specifying your model, you can indicate whether you would like to use ridge, lasso, or elastic net. We can write a general equation to minimize:

\[RSS + \lambda\left((1-\alpha)\sum_{i=1}^p\beta_j^2+\alpha\sum_{i=1}^p|\beta_j|\right)\]

lm_spec <- linear_reg() |>
  set_engine("glmnet")
  • First specify the engine. We’ll use glmnet
  • The linear_reg() function has two additional parameters, penalty and mixture
  • penalty is \(\lambda\) from our equation.
  • mixture is a number between 0 and 1 representing \(\alpha\)

Ridge, Lasso, and Elastic net

\[RSS + \lambda\left((1-\alpha)\sum_{i=1}^p\beta_j^2+\alpha\sum_{i=1}^p|\beta_j|\right)\]

What would we set mixture to in order to perform Ridge regression?

ridge_spec <- linear_reg(penalty = 100, mixture = 0) |> 
  set_engine("glmnet")

Application Exercise

  1. Set a seed set.seed(1)
  2. Create a cross validation object for the Hitters dataset
  3. Using the recipe from the previous exercise, fit the model using Ridge regression with a penalty \(\lambda\) = 300
  4. What is the estimate of the test RMSE for this model?
06:00

Ridge, Lasso, and Elastic net

\[RSS + \lambda\left((1-\alpha)\sum_{i=1}^p\beta_j^2+\alpha\sum_{i=1}^p|\beta_j|\right)\]

ridge_spec <- linear_reg(penalty = 100, mixture = 0) |> 
  set_engine("glmnet") 
lasso_spec <- linear_reg(penalty = 5, mixture = 1) |>
  set_engine("glmnet") 
enet_spec <- linear_reg(penalty = 60, mixture = 0.7) |> 
  set_engine("glmnet")

Okay, but we wanted to look at 3 different models!

ridge_spec <- linear_reg(penalty = 100, mixture = 0) |>
  set_engine("glmnet") 

results <- fit_resamples(ridge_spec,
                         preprocessor = rec,
                         resamples = Auto_cv)
lasso_spec <- linear_reg(penalty = 5, mixture = 1) |>
  set_engine("glmnet") 

results <- fit_resamples(lasso_spec,
                         preprocessor = rec,
                         resamples = Auto_cv)
elastic_spec <- linear_reg(penalty = 60, mixture = 0.7) |>
  set_engine("glmnet") 

results <- fit_resamples(elastic_spec,
                         preprocessor = rec,
                         resamples = Auto_cv)
  • 😱 this looks like copy + pasting!

tune 🎶

penalty_spec <- 
  linear_reg(penalty = tune(), mixture = tune()) |> 
  set_engine("glmnet")
  • Notice the code above has tune() for the the penalty and the mixture. Those are the things we want to vary!

tune 🎶

  • Now we need to create a grid of potential penalties ( \(\lambda\) ) and mixtures ( \(\alpha\) ) that we want to test
  • Instead of fit_resamples() we are going to use tune_grid()
grid <- expand_grid(penalty = seq(0, 100, by = 10),
                    mixture = seq(0, 1, by = 0.2))

results <- tune_grid(penalty_spec,
                     preprocessor = rec,
                     grid = grid, 
                     resamples = Auto_cv)

tune 🎶

results |>
  collect_metrics()
# A tibble: 132 × 8
   penalty mixture .metric .estimator  mean     n std_err .config              
     <dbl>   <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
 1       0       0 rmse    standard   4.25      5  0.217  Preprocessor1_Model01
 2       0       0 rsq     standard   0.710     5  0.0171 Preprocessor1_Model01
 3      10       0 rmse    standard   4.74      5  0.246  Preprocessor1_Model02
 4      10       0 rsq     standard   0.706     5  0.0193 Preprocessor1_Model02
 5      20       0 rmse    standard   5.28      5  0.255  Preprocessor1_Model03
 6      20       0 rsq     standard   0.705     5  0.0194 Preprocessor1_Model03
 7      30       0 rmse    standard   5.69      5  0.258  Preprocessor1_Model04
 8      30       0 rsq     standard   0.705     5  0.0195 Preprocessor1_Model04
 9      40       0 rmse    standard   5.99      5  0.260  Preprocessor1_Model05
10      40       0 rsq     standard   0.705     5  0.0195 Preprocessor1_Model05
# … with 122 more rows

Subset results

results |>
  collect_metrics() |>
  filter(.metric == "rmse") |>
  arrange(mean)
# A tibble: 66 × 8
   penalty mixture .metric .estimator  mean     n std_err .config              
     <dbl>   <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
 1       0     0.6 rmse    standard    4.24     5   0.207 Preprocessor1_Model34
 2       0     0.4 rmse    standard    4.24     5   0.207 Preprocessor1_Model23
 3       0     1   rmse    standard    4.24     5   0.207 Preprocessor1_Model56
 4       0     0.8 rmse    standard    4.24     5   0.207 Preprocessor1_Model45
 5       0     0.2 rmse    standard    4.24     5   0.207 Preprocessor1_Model12
 6       0     0   rmse    standard    4.25     5   0.217 Preprocessor1_Model01
 7      10     0   rmse    standard    4.74     5   0.246 Preprocessor1_Model02
 8      20     0   rmse    standard    5.28     5   0.255 Preprocessor1_Model03
 9      10     0.2 rmse    standard    5.37     5   0.258 Preprocessor1_Model13
10      30     0   rmse    standard    5.69     5   0.258 Preprocessor1_Model04
# … with 56 more rows
  • Since this is a data frame, we can do things like filter and arrange!

Subset results

results |>
  collect_metrics() |>
  filter(.metric == "rmse") |>
  arrange(mean)
# A tibble: 66 × 8
   penalty mixture .metric .estimator  mean     n std_err .config              
     <dbl>   <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
 1       0     0.6 rmse    standard    4.24     5   0.207 Preprocessor1_Model34
 2       0     0.4 rmse    standard    4.24     5   0.207 Preprocessor1_Model23
 3       0     1   rmse    standard    4.24     5   0.207 Preprocessor1_Model56
 4       0     0.8 rmse    standard    4.24     5   0.207 Preprocessor1_Model45
 5       0     0.2 rmse    standard    4.24     5   0.207 Preprocessor1_Model12
 6       0     0   rmse    standard    4.25     5   0.217 Preprocessor1_Model01
 7      10     0   rmse    standard    4.74     5   0.246 Preprocessor1_Model02
 8      20     0   rmse    standard    5.28     5   0.255 Preprocessor1_Model03
 9      10     0.2 rmse    standard    5.37     5   0.258 Preprocessor1_Model13
10      30     0   rmse    standard    5.69     5   0.258 Preprocessor1_Model04
# … with 56 more rows

Which would you choose?

results |>
  collect_metrics() |>
  filter(.metric == "rmse") |>
  ggplot(aes(penalty, mean, color = factor(mixture), group = factor(mixture))) +
  geom_line() +
  geom_point() + 
  labs(y = "RMSE")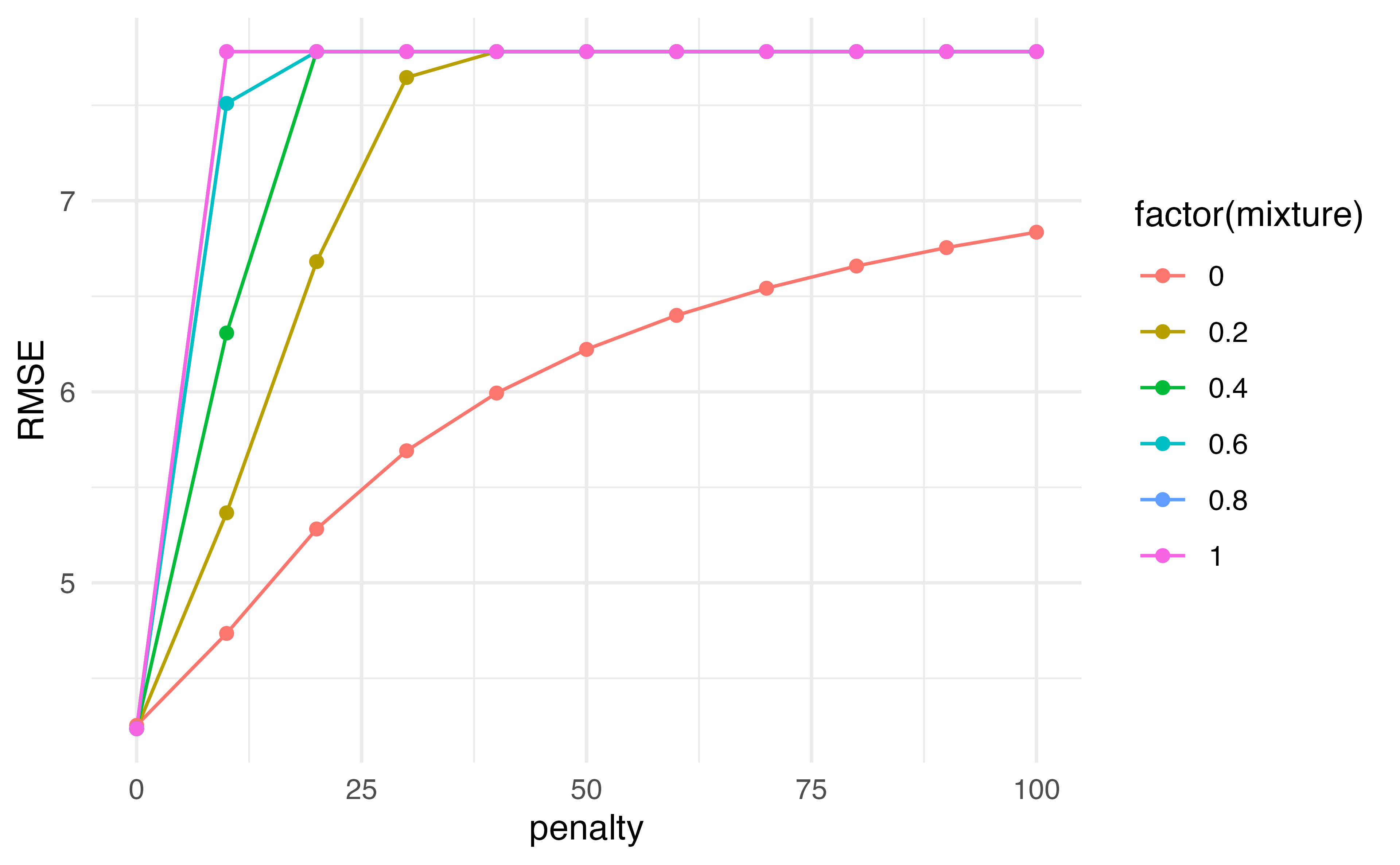

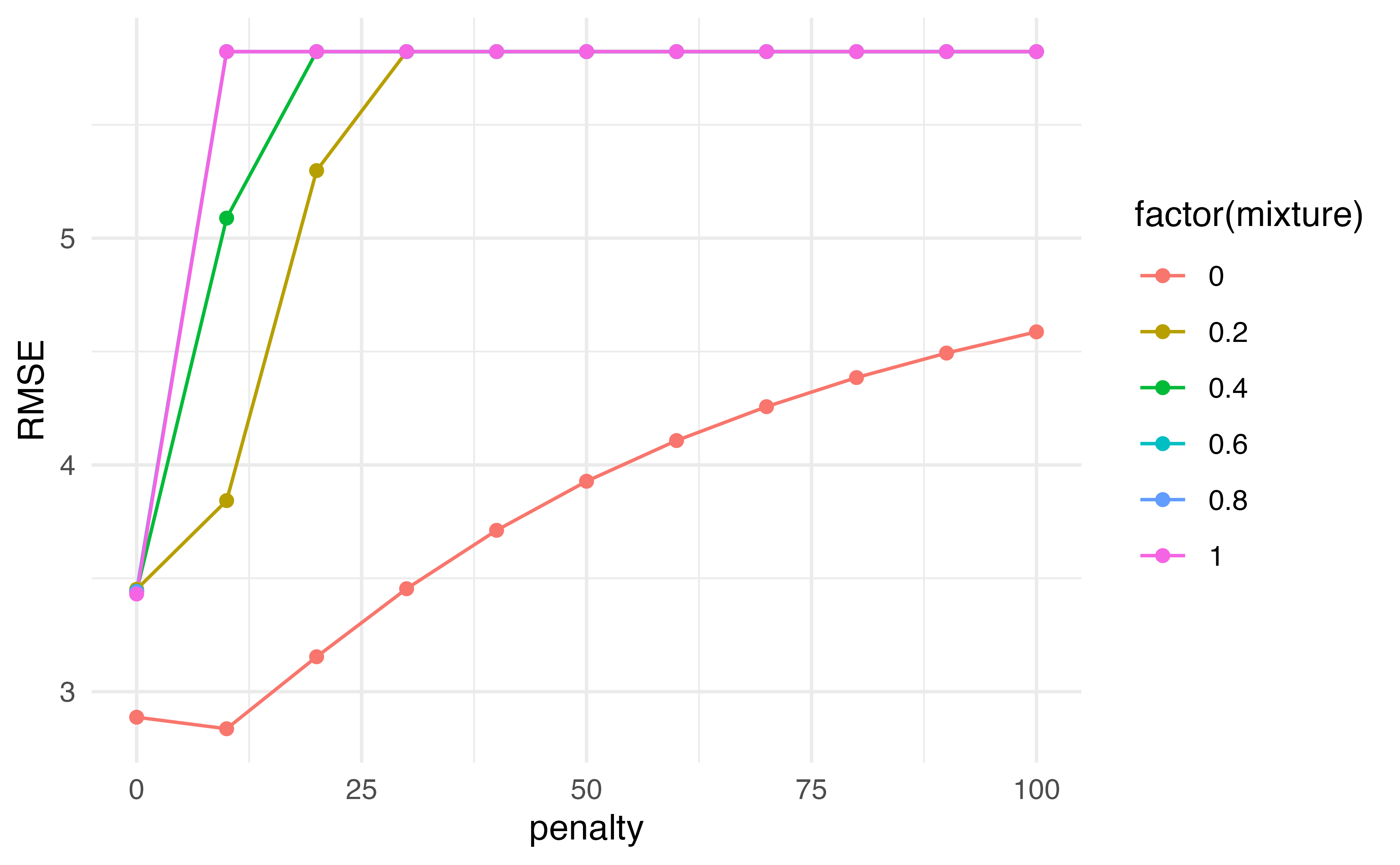
Application Exercise

  1. Using the Hitters cross validation object and recipe created in the previous exercise, use tune_grid to pick the optimal penalty and mixture values.
  2. Update the code below to create a grid that includes penalties from 0 to 50 by 1 and mixtures from 0 to 1 by 0.5.
  3. Use this grid in the tune_grid function. Then use collect_metrics and filter to only include the RSME estimates.
  4. Create a figure to examine the estimated test RMSE for the grid of penalty and mixture values – which should you choose?
grid <- expand_grid(penalty = seq(0, ----),
                    mixture = seq(0, 1, by = ----))
08:00

Putting it all together

  • Often we can use a combination of all of these tools together
  • First split our data
  • Do cross validation on just the training data to tune the parameters
  • Use last_fit() with the selected parameters, specifying the split data so that it is evaluated on the left out test sample

Putting it all together

auto_split <- initial_split(Auto, prop = 0.5)
auto_train <- training(auto_split)
auto_cv <- vfold_cv(auto_train, v = 5)

rec <- recipe(mpg ~ horsepower + displacement + weight, data = auto_train) |>
  step_scale(all_predictors())

tuning <- tune_grid(penalty_spec,
                     rec,
                     grid = grid,
                     resamples = auto_cv)

tuning |>
  collect_metrics() |>
  filter(.metric == "rmse") |>
  arrange(mean)
# A tibble: 66 × 8
   penalty mixture .metric .estimator  mean     n std_err .config              
     <dbl>   <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
 1       0     1   rmse    standard    4.52     5   0.105 Preprocessor1_Model56
 2       0     0.6 rmse    standard    4.52     5   0.105 Preprocessor1_Model34
 3       0     0.8 rmse    standard    4.52     5   0.106 Preprocessor1_Model45
 4       0     0.2 rmse    standard    4.53     5   0.104 Preprocessor1_Model12
 5       0     0.4 rmse    standard    4.53     5   0.104 Preprocessor1_Model23
 6       0     0   rmse    standard    4.54     5   0.132 Preprocessor1_Model01
 7      10     0   rmse    standard    5.01     5   0.232 Preprocessor1_Model02
 8      20     0   rmse    standard    5.54     5   0.266 Preprocessor1_Model03
 9      10     0.2 rmse    standard    5.63     5   0.271 Preprocessor1_Model13
10      30     0   rmse    standard    5.94     5   0.280 Preprocessor1_Model04
# … with 56 more rows

Putting it all together

final_spec <- linear_reg(penalty = 0, mixture = 0) |>
  set_engine("glmnet")
fit <- last_fit(final_spec, 
                rec,
                split = auto_split) 
fit |>
  collect_metrics()
# A tibble: 2 × 4
  .metric .estimator .estimate .config             
  <chr>   <chr>          <dbl> <chr>               
1 rmse    standard       4.00  Preprocessor1_Model1
2 rsq     standard       0.726 Preprocessor1_Model1

Extracting coefficients

  • We can use workflow() to combine the recipe and the model specification to pass to a fit object.
training_data <- training(auto_split)

workflow() |>
  add_recipe(rec) |>
  add_model(final_spec) |>
  fit(data = training_data) |>
  tidy()
# A tibble: 4 × 3
  term         estimate penalty
  <chr>           <dbl>   <dbl>
1 (Intercept)     43.8        0
2 horsepower      -2.13       0
3 displacement    -1.04       0
4 weight          -3.50       0

Application Exercise

  1. Using the final model specification, extract the coefficients from the model by creating a workflow
  2. Filter out any coefficients exactly equal to 0
03:00

Dr. Lucy D’Agostino McGowan adapted from Alison Hill’s Introduction to ML with the Tidyverse