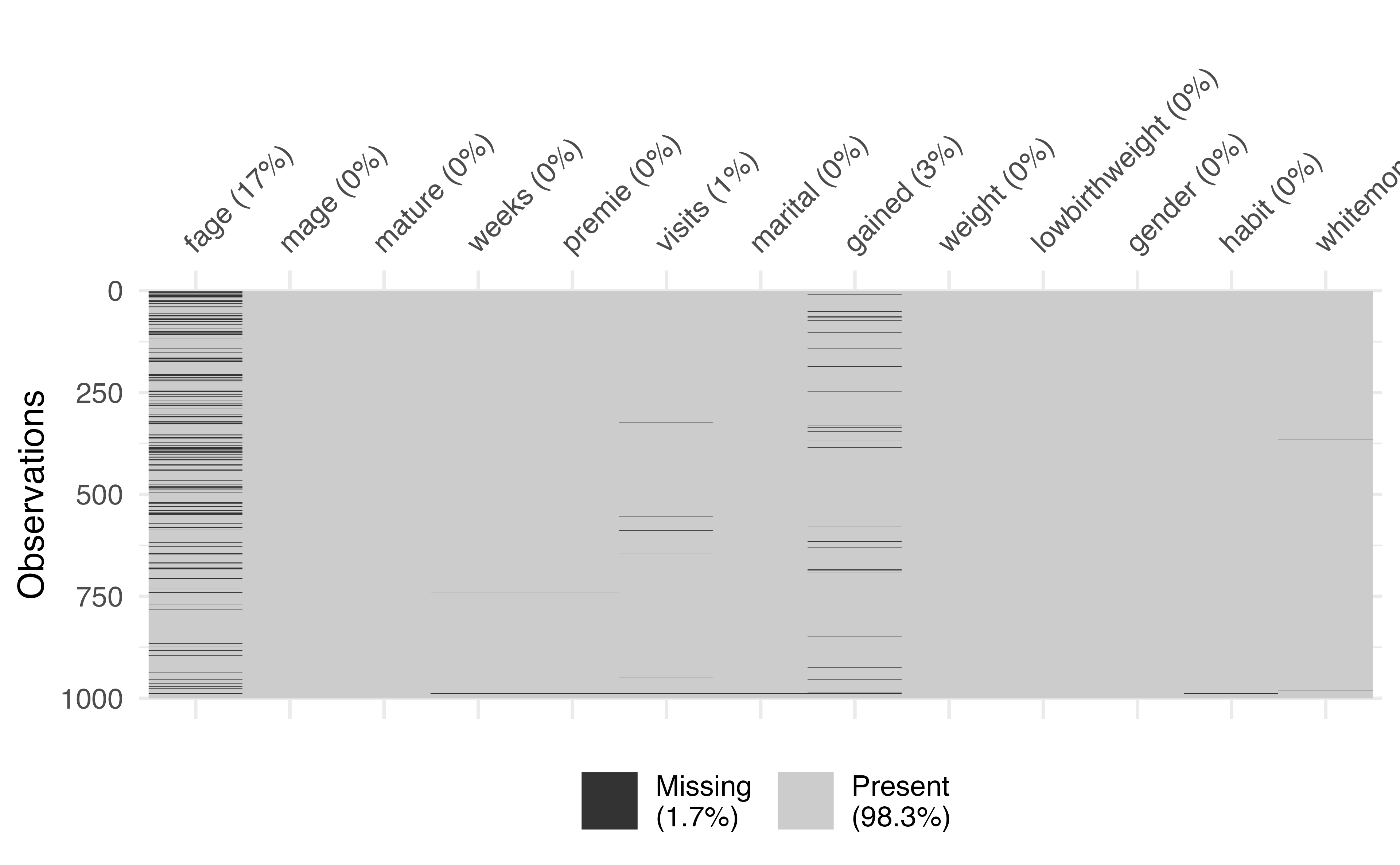
Missing Data

Lucy D’Agostino McGowan

The Data

• fage : father’s age in years.
• mage : mother’s age in years.
• mature : maturity status of mother.
• weeks : length of pregnancy in weeks.
• premie : whether the birth was classified as premature (premie) or full-term.
• visits : number of hospital visits during pregnancy.
• marital: whether mother is married or not married at time of birth.
• gained : weight gained by mother during pregnancy in lbs.
• weight : weight of the baby at birth in pounds.
• lowbirthweight: whether baby was classified as low birthweight (low) or not (not low).
• gender: biological sex of the baby, limited to f or m.
• habit : status of the mother as a nonsmoker or a smoker.
• whitemom: whether mom identifies as white or not white.

Missing data exploratory analysis

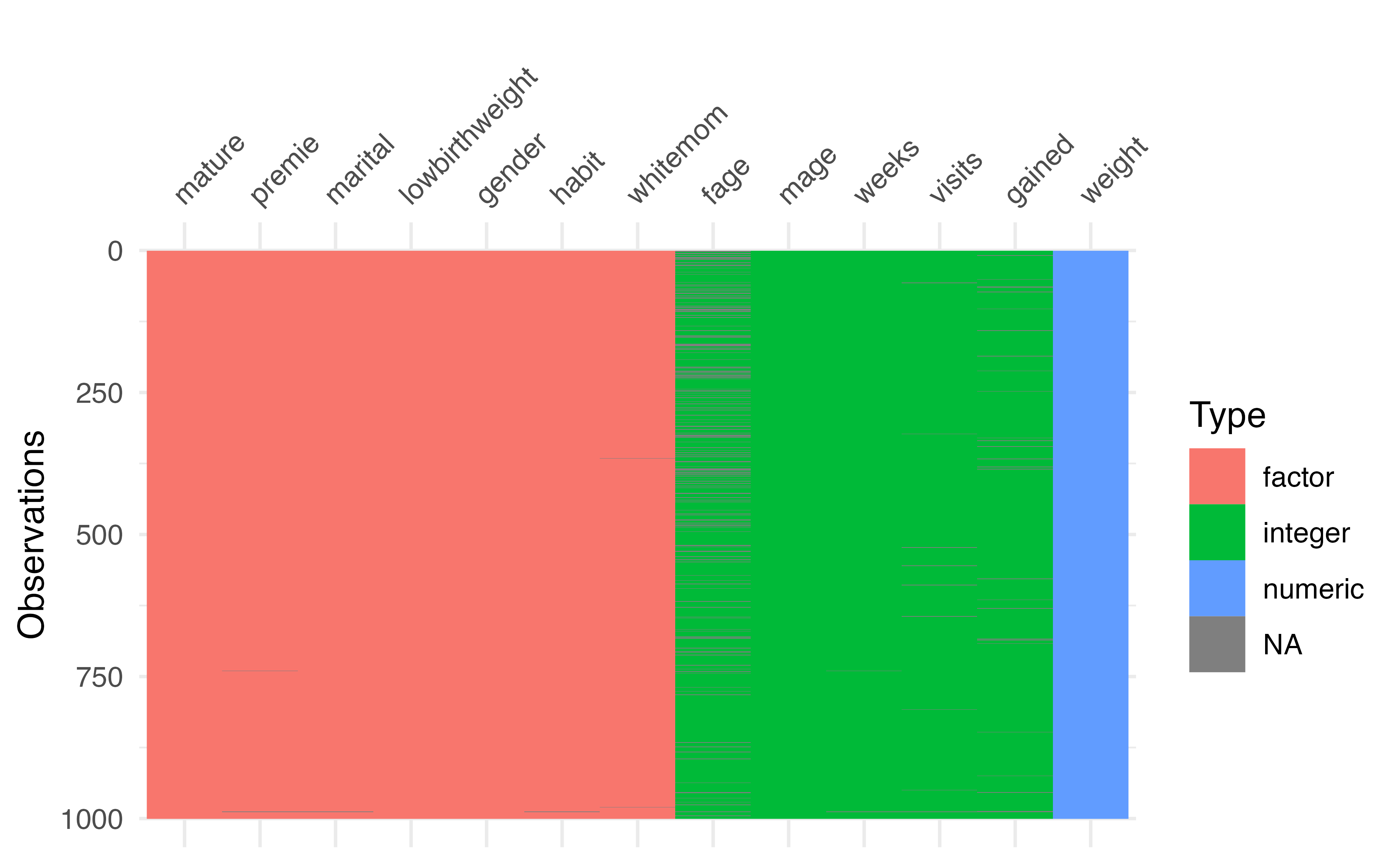
• The visdat package is a great way to visualize key information about your dataset
• Use the function vis_dat() on your dataframe to see the column types and explore missingness
  • This is especially useful for large datasets
• Use the vis_miss() function to learn more about the missing data

vis_dat()

library(visdat)
vis_dat(nc)

Which column has the most missing data?

vis_miss()

vis_miss(nc)

What do we do?

There are three typical approaches:

• Complete Case Analysis
• Available Case Analysis
• Imputation

Complete Case Analysis

Complete Case Analysis

• This is probably what you have done most often
• This means we eliminate all rows in the dataset that contain any missing data
• The only rows we use are the complete rows, with no missing data

Complete Case Analysis

Advantage: It is easy!

• The first step is to create a dataset that only includes rows that are fully observed

nc_complete_case <- nc |>
  drop_na()

## OR

library(tidymodels)
recipe_nc <- recipe(lowbirthweight ~ ., data = nc) |>
  step_naomit(everything()) # this is actual available case behind the scenes

NOTE It is important that you hold on to the original data somewhere when doing complete case analysis, we may need to go back and look at the rows we dropped.

Complete case analysis

When doing complete cases analysis, it is important to always note how many observations are dropped.

n_cc <- nrow(nc_complete_case)
n <- nrow(nc)
n - n_cc

[1] 200

(n - n_cc) / n

[1] 0.2

• Here we are dropping 200 rows, losing 20% of the data

Disadvantages of Complete Case Analysis

What issues might there be with simply deleting 20% of your sample?

• We reduce our sample size
• We could lose the representative nature of our data
  • What if the data is missing for a reason?
  • What if a particular group of people refused to answer a question, so by conducting a complete case analysis we completely remove that group of people from the data set?

What assumptions are we making?

• When doing a complete case analysis, we assume the data is missing completely at random
• This means that when we remove all the rows with missing data, our sample is still representative of the population – a very strong assumption!

Available Case Analysis

• Suppose there are 30 variables, but we only need to use 25 in our analysis
• Available case analysis means we ignore any missing data in the 5 variables we don’t plan to use and eliminate all rows with missing data in our desired 25 variables

Available Case Analysis

Advantages: Same as complete case analysis (fast and easy!)

Disadvantages: Same as complete case analysis (the variables we are including must be missing completely at random)

Available Case Analysis

nc_available_case <- nc |>
  drop_na(fage, mage, marital, lowbirthweight)

## OR

recipe_nc <- recipe(lowbirthweight ~ mage + fage + marital, data = nc) |>
  step_naomit(all_predictors(), all_outcomes()) 

n_ac <- nrow(nc_available_case)
n - n_ac

[1] 171

(n - n_ac) / n

[1] 0.171

Alternative

Okay, but what about when neither complete case analysis or available case analysis is appropriate?

• In these situations, we are going to consider imputation

• Imputation is the process of estimating the missing values to create a completed version of the data set.

Imputation

Imputation

To impute all the missing values in this data set, we are going to

1. Estimate values for all the missing values in the original data set
2. Fill in the missing data with these estimates. This is called completing the data
3. End up with a data set that has the same dimensions as the original nc data set, but with no missing data.
4. Proceed with our modeling.

Getting started

There are a lot of techniques we can use for imputation.

• The hardest step in this process is deciding which technique might be appropriate

• We are going to explore a few commonly used techniques, and discuss the pros and cons of each

fage: Father’s Age

• Let’s look at one variable with a lot of missing data: fage
• There are 171 rows that are missing this variable
• For example, here is row 1:

fage: Father’s Age

• Let’s look at one variable with a lot of missing data: fage
• There are 171 rows that are missing this variable
• For example, here is row 1:

# A tibble: 1 × 13
   fage  mage mature    weeks premie visits marital gained weight lowbi…¹ gender
  <int> <int> <fct>     <int> <fct>   <int> <fct>    <int>  <dbl> <fct>   <fct> 
1    NA    13 younger …    39 full …     10 married     38   7.63 not low male  
# … with 2 more variables: habit <fct>, whitemom <fct>, and abbreviated
#   variable name ¹​lowbirthweight

• We need to decide how to impute (estimate the missing values) for father’s age

Technique 1: Unconditional Mean Imputation

• One of the simplest techniques for imputing such values is called unconditional mean imputation, or UMI.
• This imputation technique involves filling in missing values by looking at all rows that have observed information for the variable of interest, and computing the mean of that variable.
• We then impute all rows that are missing the variable by plugging in the mean.
• The idea behind this technique is that if we don’t know what a missing data value should be, it may be reasonable to just plug in the average value.

Technique 1: Unconditional Mean Imputation

For our variable of interest, fage, we can conduct unconditional mean imputation (UMI) by

1. taking all of the data point for which fage is observed
2. computing the mean and
3. replacing all missing fage values with this mean.

• This will yield a data set that is completed, i.e., has no missing data, in fage

Technique 1: Unconditional Mean Imputation

recipe_nc <- recipe(lowbirthweight ~ ., data = nc) |>
  step_impute_mean(fage)

Technique 1: Unconditional Mean Imputation

Behind the scenes (in practice you don’t need the code below, just showing what the recipe is doing)

nc |>
  summarise(mean_fage = mean(fage, na.rm = TRUE))

# A tibble: 1 × 1
  mean_fage
      <dbl>
1      30.3

nc_mean_impute <- nc |>
  mutate(
    imputed = is.na(fage),
    fage = case_when(
    imputed ~ 30.25573,
    TRUE ~ as.numeric(fage)
  ))

nc_mean_impute %>%
  slice(1)

# A tibble: 1 × 14
   fage  mage mature    weeks premie visits marital gained weight lowbi…¹ gender
  <dbl> <int> <fct>     <int> <fct>   <int> <fct>    <int>  <dbl> <fct>   <fct> 
1  30.3    13 younger …    39 full …     10 married     38   7.63 not low male  
# … with 3 more variables: habit <fct>, whitemom <fct>, imputed <lgl>, and
#   abbreviated variable name ¹​lowbirthweight

Checking our imputations

Once we have completed an imputation process, our next step is ALWAYS to check

• To make sure we actually filled in all the missing values and
• To check to see how these imputations compare to the observed data.
• Did we impute something completely ridiculous, or something that looks reasonable?

Checking our imputations

## Imputed data
nc_mean_imputation <- prep(recipe_nc) |>
  bake(new_data = nc)

nc_mean_imputation |>
  summarise(mean_fage = mean(fage),
            sd_fage = sd(fage))

# A tibble: 1 × 2
  mean_fage sd_fage
      <dbl>   <dbl>
1      30.2    6.16

## Complete case data
nc |>
  drop_na(fage) |>
  summarise(mean_fage = mean(fage),
            sd_fage = sd(fage))

# A tibble: 1 × 2
  mean_fage sd_fage
      <dbl>   <dbl>
1      30.3    6.76

Checking our impuations

• Why didn’t the mean change?
• How was the standard deviation different?

Considerations: Unconditional Mean Imputation

• Our imputed values were all at the mean
• This means that we put additional rows exactly 0 standard deviations from the mean
  • Standard deviation describes how much we’d expect an average data point to vary from the mean
  • Our mean-imputed data set will have a smaller standard deviation than the observed data (more rows are actually exactly at the mean – we did that! so teh average distance from the mean is smaller)
• Therefore, unconditional mean imputation generally underestiamtes the variability in the data

Considerations: Unconditional Mean Imputation

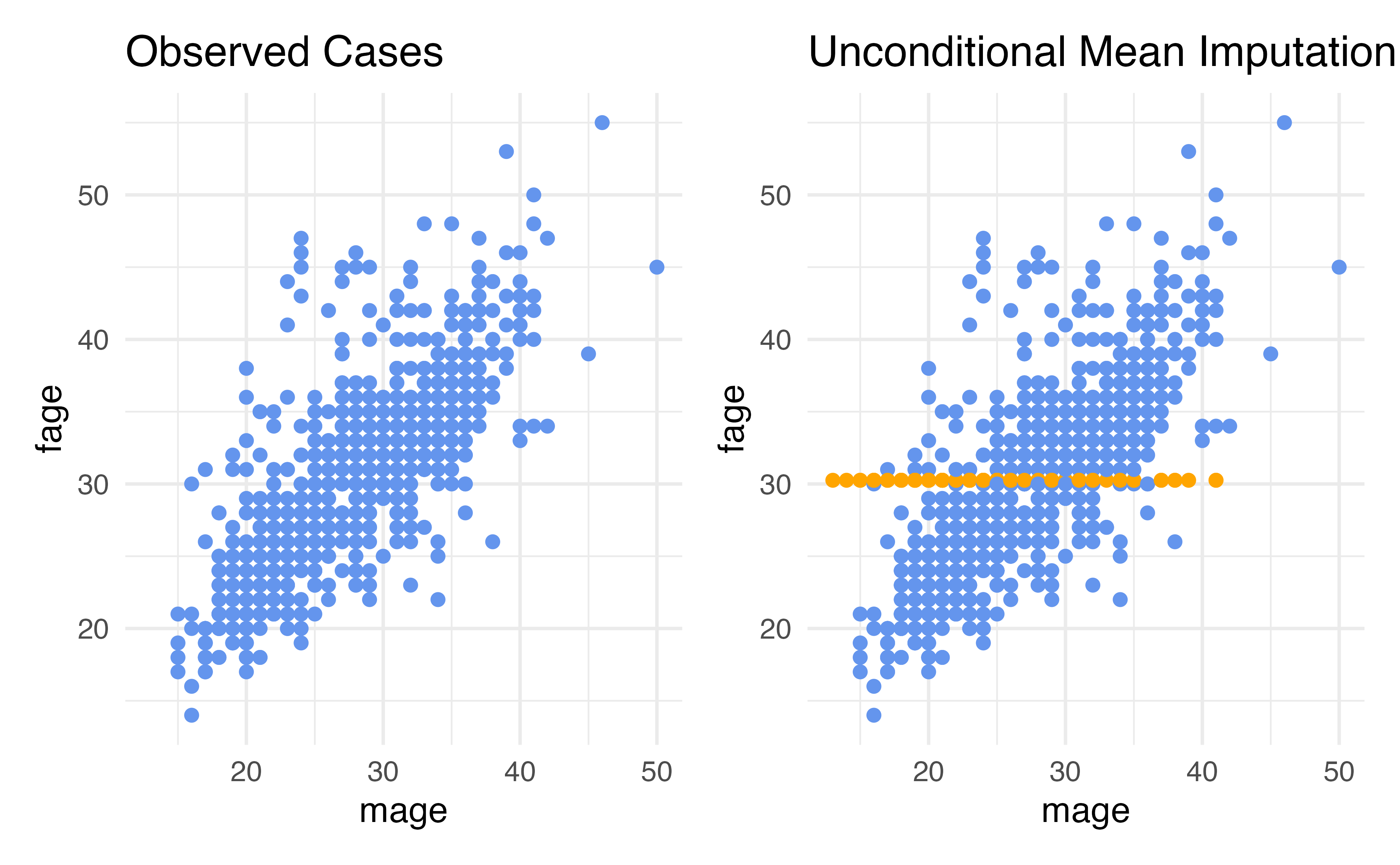
Disadvantages: Unconditional Mean Imputation

• Our imputations do not reflect the relationship in the data that exists between fage and mage
• This is because we did not include this relationship as part of our imputation strategy!
• UMI considers only the marginal distribution of the variable being imputed.
• It completely ignores the fact that values of fage might be related to another variable present in the data set.
• As a result, using unconditional mean imputation often results in a distortion of conditional distributions in the data

Considerations for Unconditional Mean Imputation

• Pros: It is fast and easy to compute, you can use all observed data

• Cons:

  • It underestimates the variability in the data
  • It often distorts conditional distributions in the data
  • It relies on the data being missing completely at random

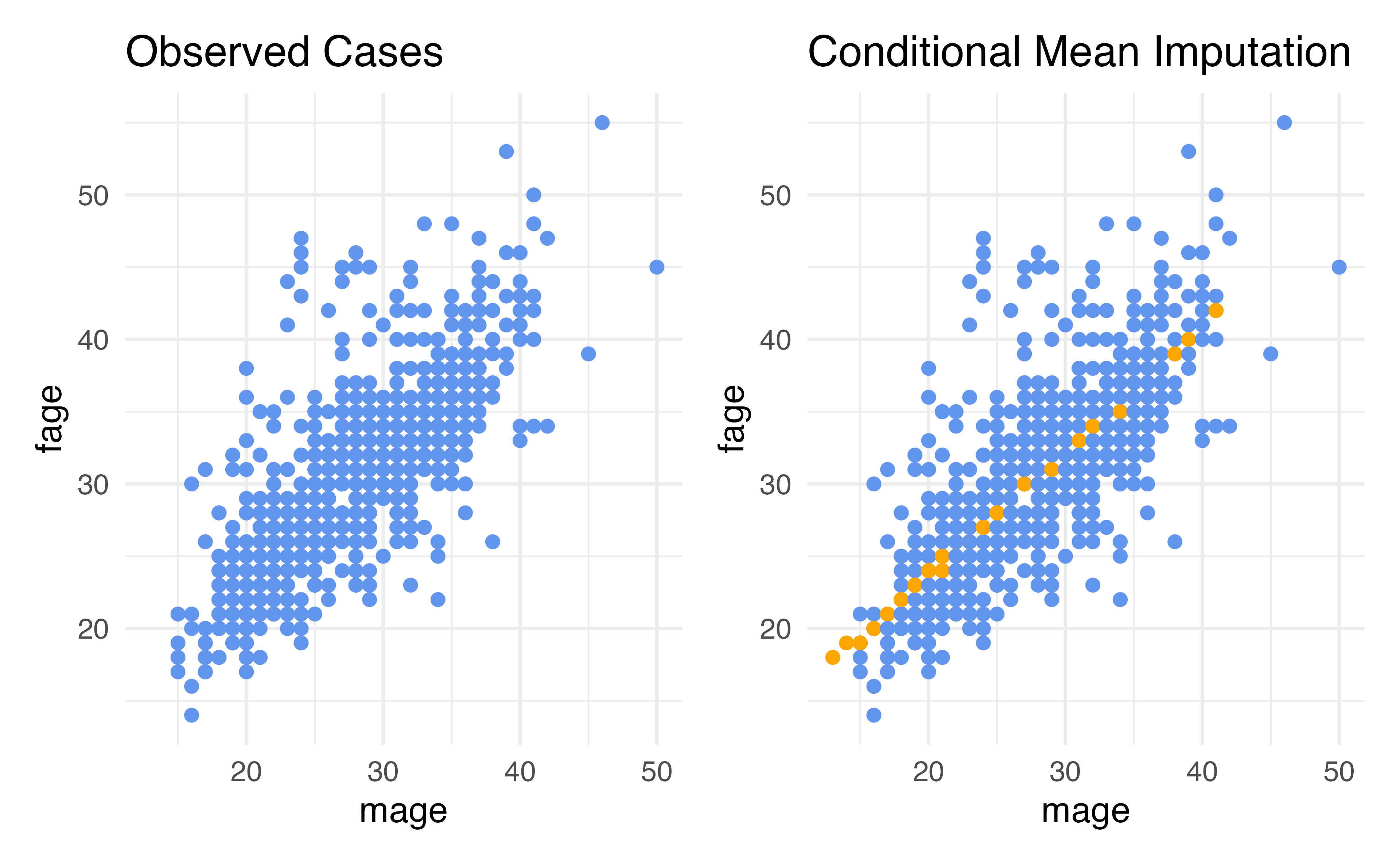
Conditional Mean Imputation

Conditional Mean Imputation

• Rather than computing the marginal mean and putting that in for our missing values, we could calculate a conditional mean, a mean that conditions on our other variables
• How do we calculate conditional means?
• Linear regression is the simplest way!

Conditional Mean Imputation

recipe_nc <- recipe(lowbirthweight ~ ., data = nc) |>
  step_impute_linear(fage, impute_with = imp_vars(mage))

recipe_nc

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         12

Operations:

Linear regression imputation for fage

Conditional Mean Imputation

Behind the scenes (in practice you don’t need the code below, just showing what the recipe is doing)

nc_cmean_impute <- fit(linear_reg(),
    fage ~ mage,
    data = nc) |>
  predict(new_data = nc) |>
  bind_cols(nc) |>
  mutate(
    imputed = is.na(fage),
    fage = case_when(
    imputed ~ .pred,
    TRUE ~ as.numeric(fage)
  ))

nc_cmean_impute

# A tibble: 1,000 × 15
   .pred  fage  mage mature    weeks premie visits marital gained weight lowbi…¹
   <dbl> <dbl> <int> <fct>     <int> <fct>   <int> <fct>    <int>  <dbl> <fct>  
 1  17.8  17.8    13 younger …    39 full …     10 married     38   7.63 not low
 2  18.6  18.6    14 younger …    42 full …     15 married     20   7.88 not low
 3  19.5  19      15 younger …    37 full …     11 married     38   6.63 not low
 4  19.5  21      15 younger …    41 full …      6 married     34   8    not low
 5  19.5  19.5    15 younger …    39 full …      9 married     27   6.38 not low
 6  19.5  19.5    15 younger …    38 full …     19 married     22   5.38 low    
 7  19.5  18      15 younger …    37 full …     12 married     76   8.44 not low
 8  19.5  17      15 younger …    35 premie      5 married     15   4.69 low    
 9  20.3  20.3    16 younger …    38 full …      9 married     NA   8.81 not low
10  20.3  20      16 younger …    37 full …     13 married     52   6.94 not low
# … with 990 more rows, 4 more variables: gender <fct>, habit <fct>,
#   whitemom <fct>, imputed <lgl>, and abbreviated variable name
#   ¹​lowbirthweight

Conditional Mean Imputation

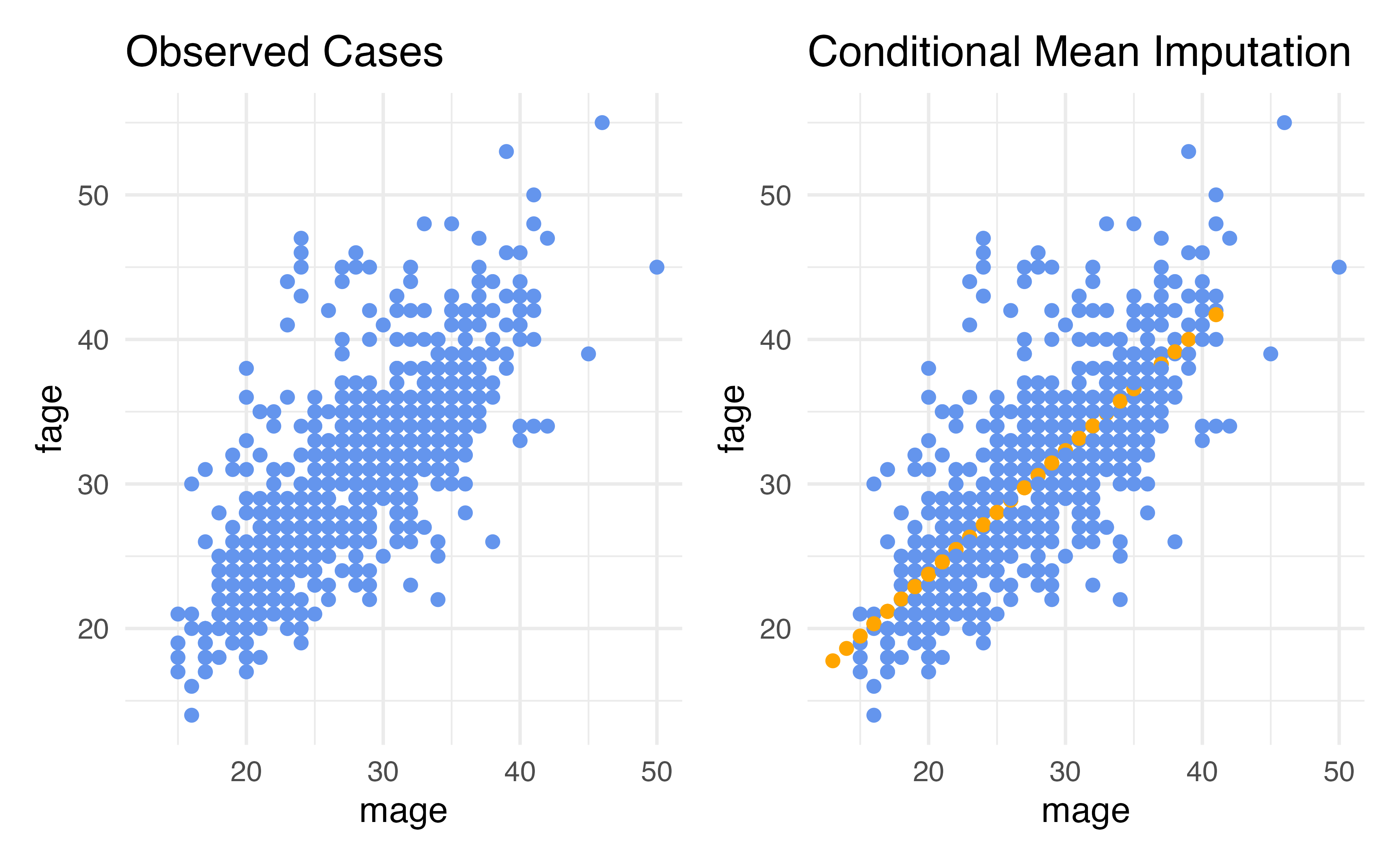
Summary statistics

nc_cmean_imputation <- prep(recipe_nc) |>
  bake(new_data = nc)

nc_cmean_imputation |>
  summarise(mean_fage = mean(fage),
            sd_fage = sd(fage))

# A tibble: 1 × 2
  mean_fage sd_fage
      <dbl>   <dbl>
1      29.7    6.57

nc |>
  drop_na(fage, mage) |>
  summarise(mean_fage = mean(fage),
            sd_fage = sd(fage))

# A tibble: 1 × 2
  mean_fage sd_fage
      <dbl>   <dbl>
1      30.3    6.76

What if we want to include more variables?

• What if we think fage is actually conditional on more than just mage?

What if we want to include more variables?

• What if we think fage is actually conditional on more than just mage?

recipe_nc <- recipe(lowbirthweight ~ ., data = nc) |>
  step_impute_mode(marital) |>
  step_impute_linear(fage, impute_with = imp_vars(mage, marital))

recipe_nc

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         12

Operations:

Mode imputation for marital
Linear regression imputation for fage

Conditional Mean Imputation

Conditional Mean Imputation

• The tidymodels default is to try to impute values using all other predictors
• The problem is in order to use this method, the values must not be missing for the other predictors (which is often not the case!)
• Let’s see how this errors

Conditional Mean Imputation

recipe_nc <- recipe(lowbirthweight ~ ., data = nc) |>
  step_impute_linear(fage, impute_with = imp_vars(all_predictors()))

wf <- workflow() |>
add_recipe(recipe_nc) |>
  add_model(logistic_reg())

fit(wf, data = nc)

Warning: 
          There were missing values in the predictor(s) used to impute;
          imputation did not occur.
        

Warning: glm.fit: algorithm did not converge

Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
1 Recipe Step

• step_impute_linear()

── Model ───────────────────────────────────────────────────────────────────────

Call:  stats::glm(formula = ..y ~ ., family = stats::binomial, data = data)

Coefficients:
       (Intercept)                fage                mage   matureyounger mom  
        -1499.5824             -2.1897              5.1293             44.8299  
             weeks        premiepremie              visits  maritalnot married  
            5.4982             15.0877             -2.6857              2.3088  
            gained              weight          gendermale         habitsmoker  
           -0.3773            221.9656             -6.9561            -12.8116  
     whitemomwhite  
          -11.0732  

Degrees of Freedom: 799 Total (i.e. Null);  787 Residual
  (200 observations deleted due to missingness)
Null Deviance:      493.3 
Residual Deviance: 7.287e-07    AIC: 26

Advantages: Conditional Mean (Regression) Imputation

• Our data can be conditionally missing at random – this means that the missingness only needs to be random conditional on the variables that we have included in our imputation model
• The variability to closer to what it should be compared to just mean imputation

Disadvantages: Regression Imputation

• We need to specify the conditional relationships
• So far, we’ve only talked about linear regression, meaning this method only works for continuous variables (it turns out you can use logistic for categorical variables, but then you need to specify a separate imputation method for each type of variable, this can be a lot depending on the size of your data!)
• The other variables we use for imputation need to not be missing

Conditional Imputation: KNN

• We can use another approach that is more flexible and more forgiving to missing data in the other predictors: K-Nearest-Neighbor
• The steps:

1. Using all predictors requested, calculate distances between observations (this uses a method called “Gower’s distance” which can be used for both continuous and categorical data YAY)
2. Determine “nearest neighbors”, that is other observations that are the closest to you in terms of distance calculated in (1)
3. The mode of the nearest neighbors will be filled in for categorical variables and the mean will be filled in for continuous

Conditional Imputation: KNN

recipe_nc <- recipe(lowbirthweight ~ ., data = nc) |>
  step_impute_knn(fage, impute_with = imp_vars(all_predictors()))

## these are the same

recipe_nc <- recipe(lowbirthweight ~ ., data = nc) |>
  step_impute_knn(fage)

Conditional Imputation: KNN

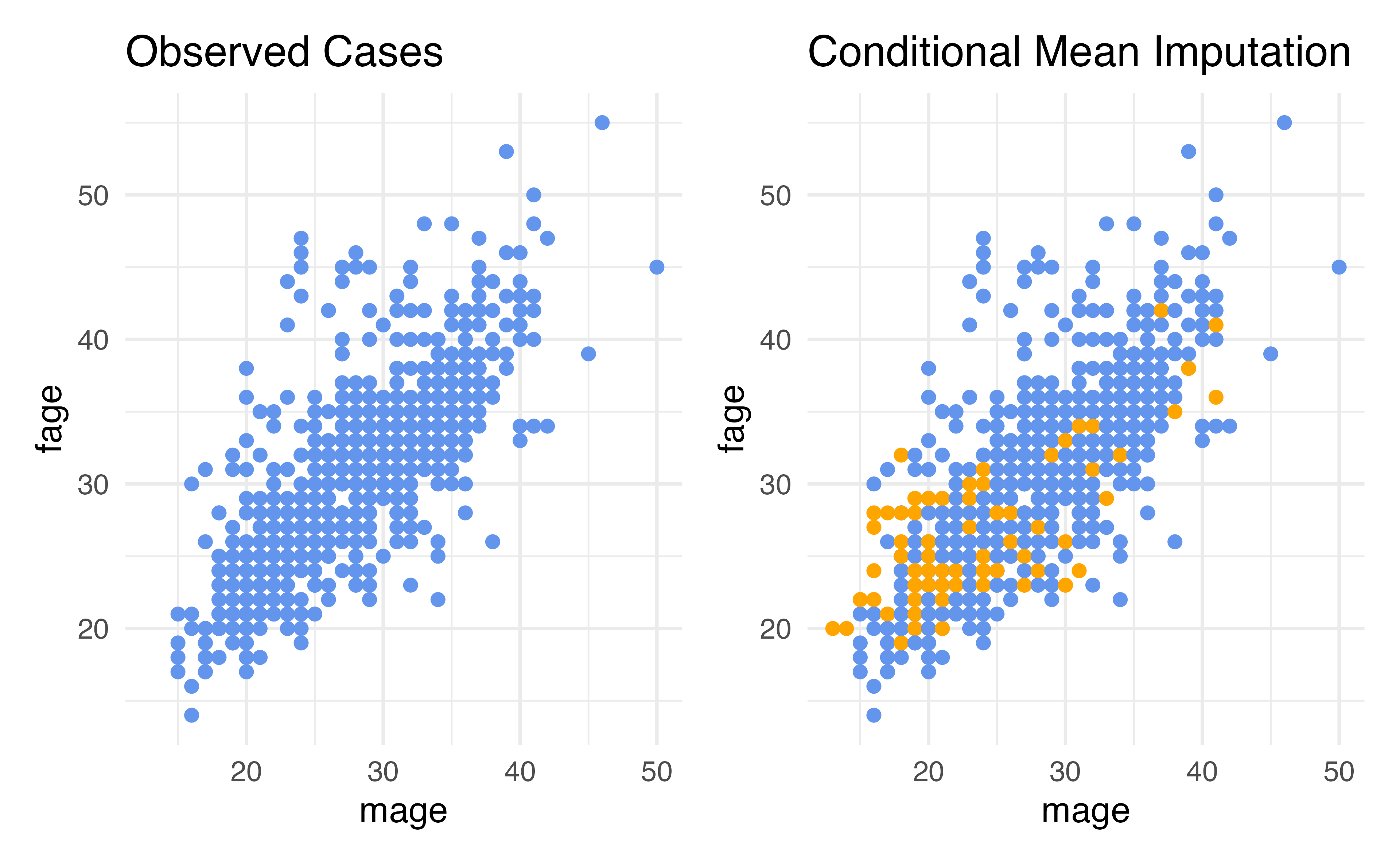
Checking summary statistics

nc_knn_impute <- prep(recipe_nc) |>
  bake(new_data = nc)

nc_knn_impute|>
  summarise(mean_fage = mean(fage),
            sd_fage = sd(fage))

# A tibble: 1 × 2
  mean_fage sd_fage
      <dbl>   <dbl>
1      29.6    6.60

nc |>
  drop_na(fage) |>
  summarise(mean_fage = mean(fage),
            sd_fage = sd(fage))

# A tibble: 1 × 2
  mean_fage sd_fage
      <dbl>   <dbl>
1      30.3    6.76

Advantages: Conditional Imputation: KNN

• Our data can be conditionally missing at random – this means that the missingness only needs to be random conditional on the variables that we have included in our imputation model
• The variability to closer to what it should be compared to just mean imputation
• The method allows for either continuous or categorical variables to be imputed using the same technique
• The other variables we are using can be missing as long as they are not mostly missing within each of the K neighbors that end up being chosen (for small percentages of missingess this is reasonable)

Disadvantages: KNN Imputation

• We need to specify the conditional relationships (can default to all predictors, though)
• Doesn’t account for the full potential variability (we need more advanced techniques like multiple imputation for that)

Advanced techniques

• Chained imputation
• Multiple imputation
• Multivariate Imputations by Chained Equations (MICE)
  • mice package in R is a nice one for this