Non-linearity

Lucy D’Agostino McGowan

Non-linear relationships

What have we used so far to deal with non-linear relationships?

  • Hint: What did you use in Lab 02?
  • Polynomials!

Polynomials

\[y_i = \beta_0 + \beta_1x_i + \beta_2x_i^2+\beta_3x_i^3 \dots + \beta_dx_i^d+\epsilon_i\]

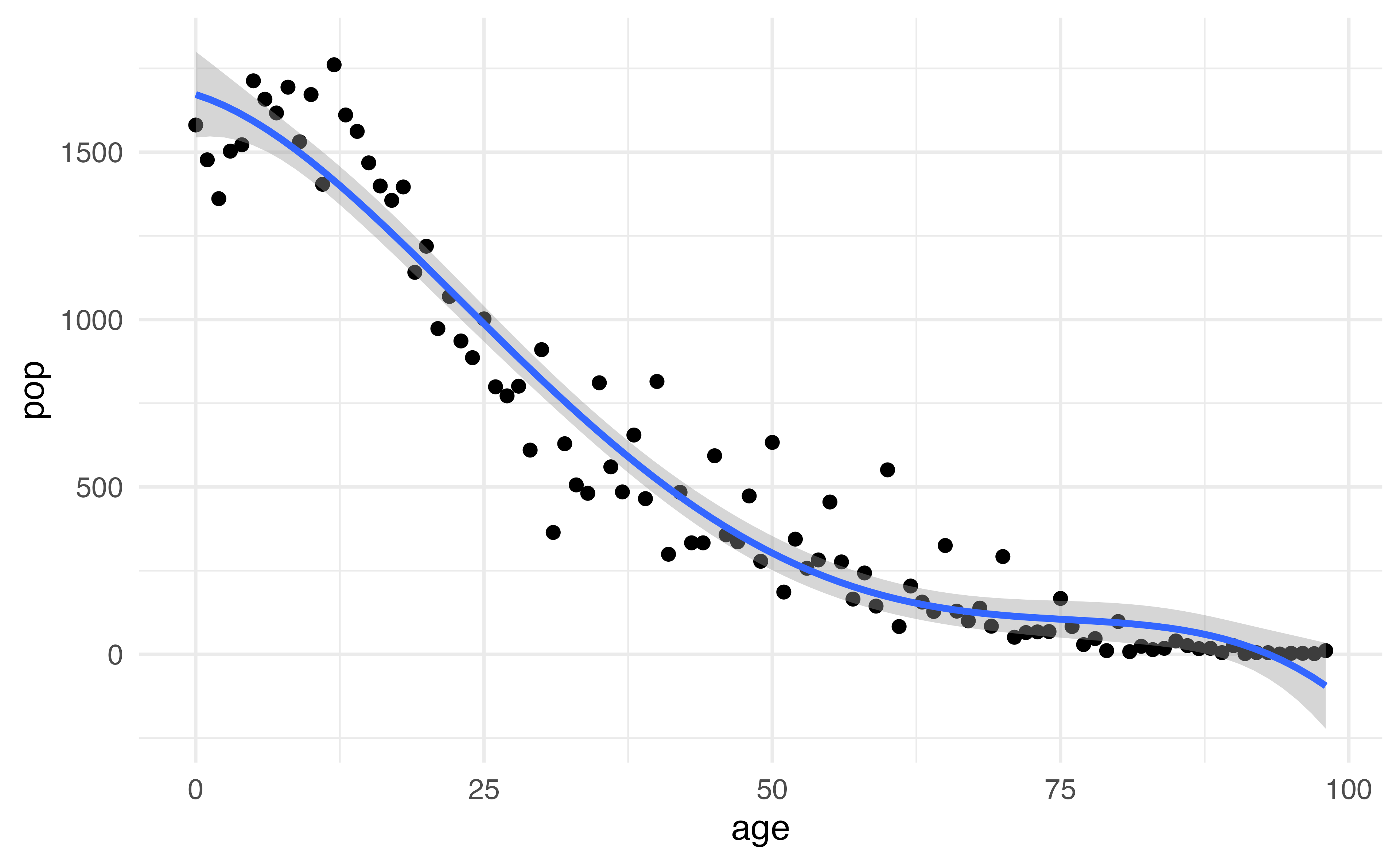
This is data from the Columbia World Fertility Survey (1975-76) to examine household compositions

Polynomials

\[y_i = \beta_0 + \beta_1x_i + \beta_2x_i^2+\beta_3x_i^3 \dots + \beta_dx_i^d+\epsilon_i\]

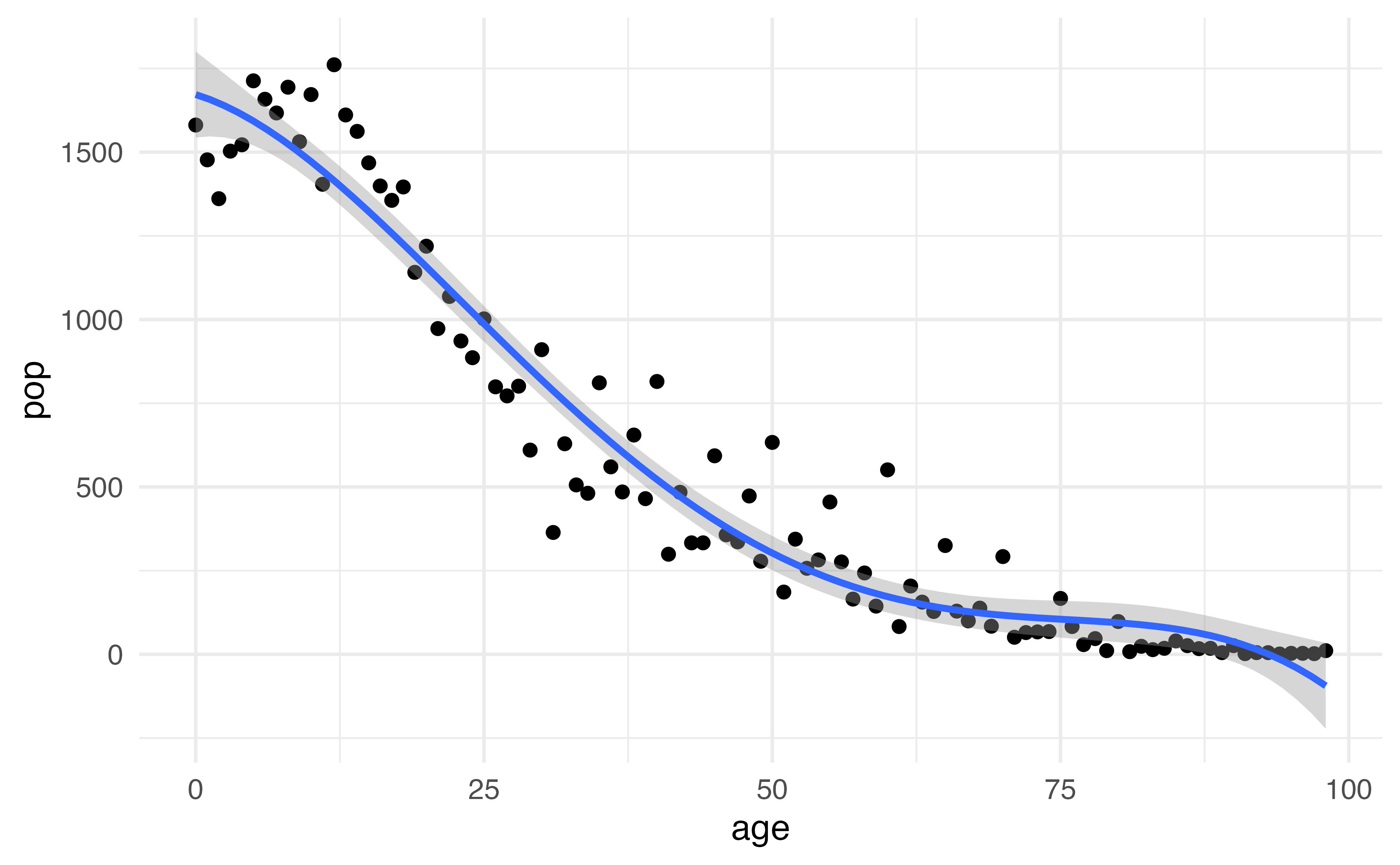
  • Fit here with a 4th degree polynomial

How is it done?

  • New variables are created ( \(X_1 = X\), \(X_2 = X^2\), \(X_3 = X^3\), etc) and treated as multiple linear regression
  • We are not interested in the individual coefficients, we are interested in how a specific \(x\) value behaves
  • \(\hat{f}(x_0) = \hat\beta_0 + \hat\beta_1x_0 + \hat\beta_2x_0^2 + \hat\beta_3x_0^3 + \hat\beta_4x_0^4\)
  • or more often a change between two values, \(a\) and \(b\)
  • \(\hat{f}(b) -\hat{f}(a) = \hat\beta_1b + \hat\beta_2b^2 + \hat\beta_3b^3 + \hat\beta_4b^4 - \hat\beta_1a - \hat\beta_2a^2 - \hat\beta_3a^3 -\hat\beta_4a^4\)
  • \(\hat{f}(b) -\hat{f}(a) =\hat\beta_1(b-a) + \hat\beta_2(b^2-a^2)+\hat\beta_3(b^3-a^3)+\hat\beta_4(b^4-a^4)\)

Polynomial Regression

\[\hat{f}(b) -\hat{f}(a) =\hat\beta_1(b-a) + \hat\beta_2(b^2-a^2)+\hat\beta_3(b^3-a^3)+\hat\beta_4(b^4-a^4)\]

How do you pick \(a\) and \(b\)?

  • If given no other information, a sensible choice may be the 25th and 75th percentiles of \(x\)

Polynomial Regression

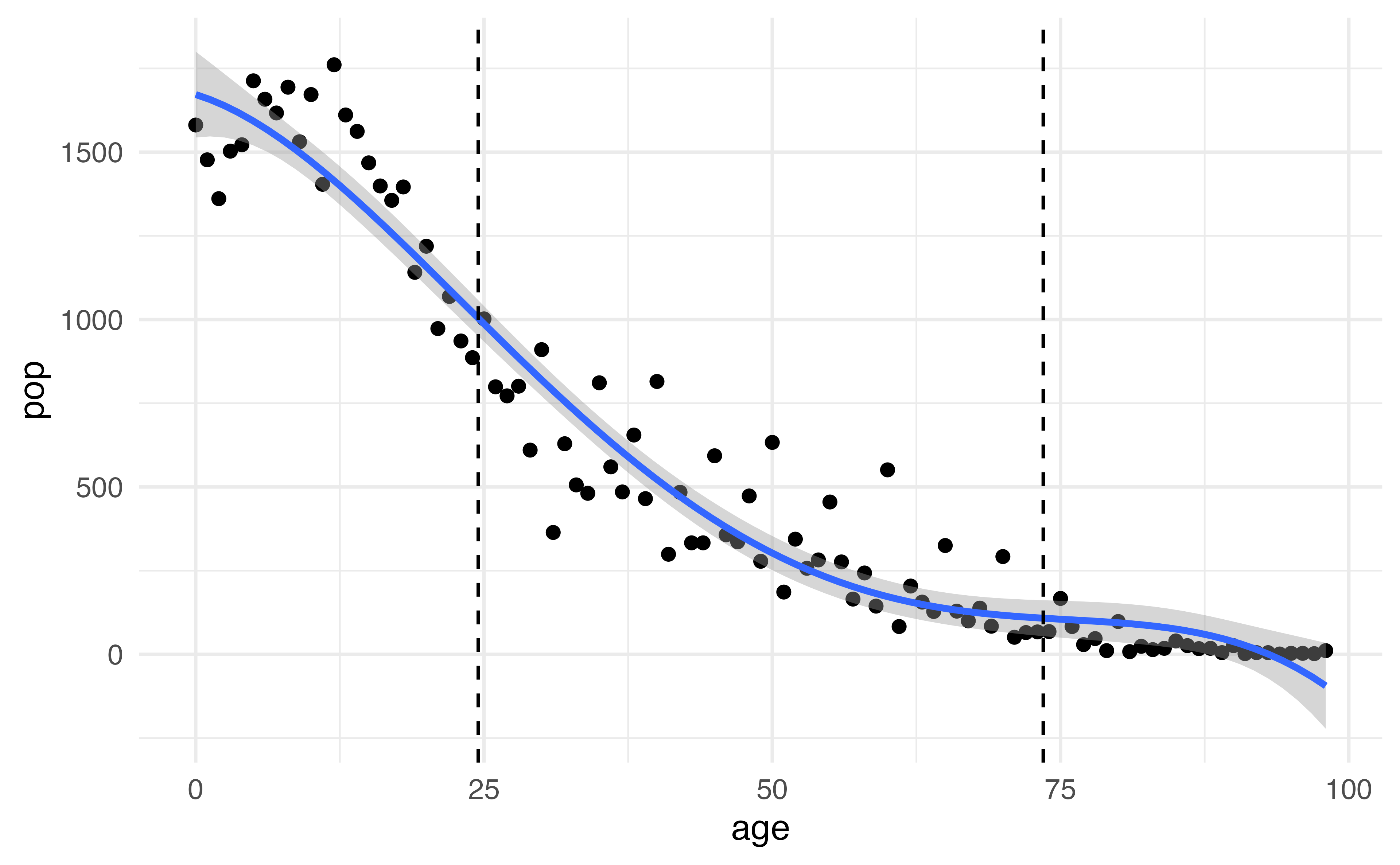
Application Exercise

\[pop = \beta_0 + \beta_1age + \beta_2age^2 + \beta_3age^3 +\beta_4age^4+ \epsilon\]

Using the information below, write out the equation to predicted change in population from a change in age from the 25th percentile (24.5) to a 75th percentile (73.5).

term estimate std.error statistic p.value
(Intercept) 1672.0854 64.5606 25.8995 0.0000
age -10.6429 9.2268 -1.1535 0.2516
I(age^2) -1.1427 0.3857 -2.9627 0.0039
I(age^3) 0.0216 0.0059 3.6498 0.0004
I(age^4) -0.0001 0.0000 -3.6540 0.0004
03:00

Choosing \(d\)

\[y_i = \beta_0 + \beta_1x_i + \beta_2x_i^2+\beta_3x_i^3 \dots + \beta_dx_i^d+\epsilon_i\]

Either:

  • Pre-specify \(d\) (before looking 👀 at your data!)
  • Use cross-validation to pick \(d\)

Why?

Polynomial Regression

Polynomials have notoriously bad tail behavior (so they can be bad for extrapolation)

What does this mean?

Step functions

Another way to create a transformation is to cut the variable into distinct regions

\[C_1(X) = I(X < 35), C_2(X) = I(35\leq X<65), C_3(X) = I(X \geq 65)\]

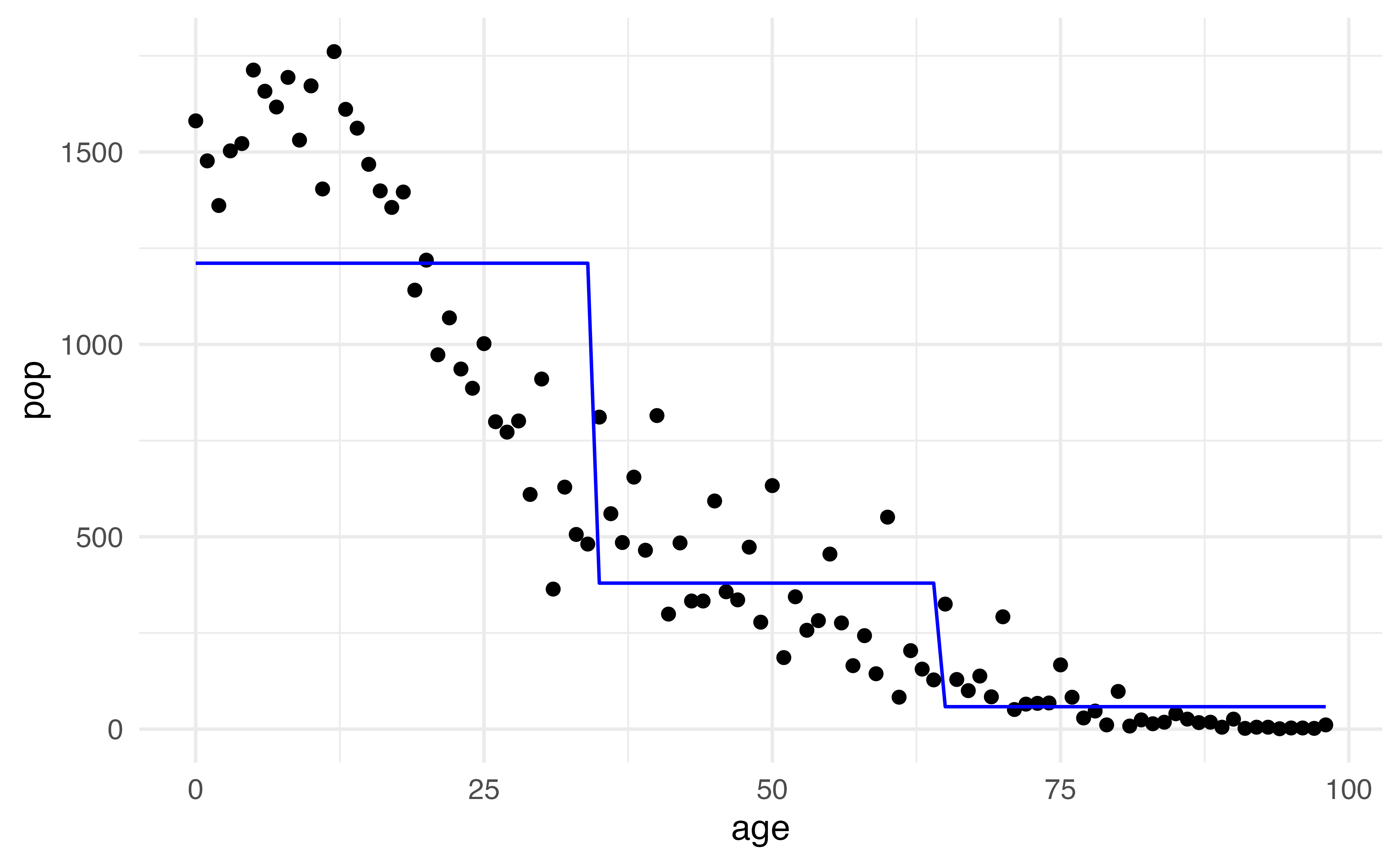
Step functions

  • Create dummy variables for each group
  • Include each of these variables in multiple regression
  • The choice of cutpoints or knots can be problematic (and make a big difference!)

Step functions

\[C_1(X) = I(X < 35), C_2(X) = I(35\leq X<65), C_3(X) = I(X \geq 65)\]

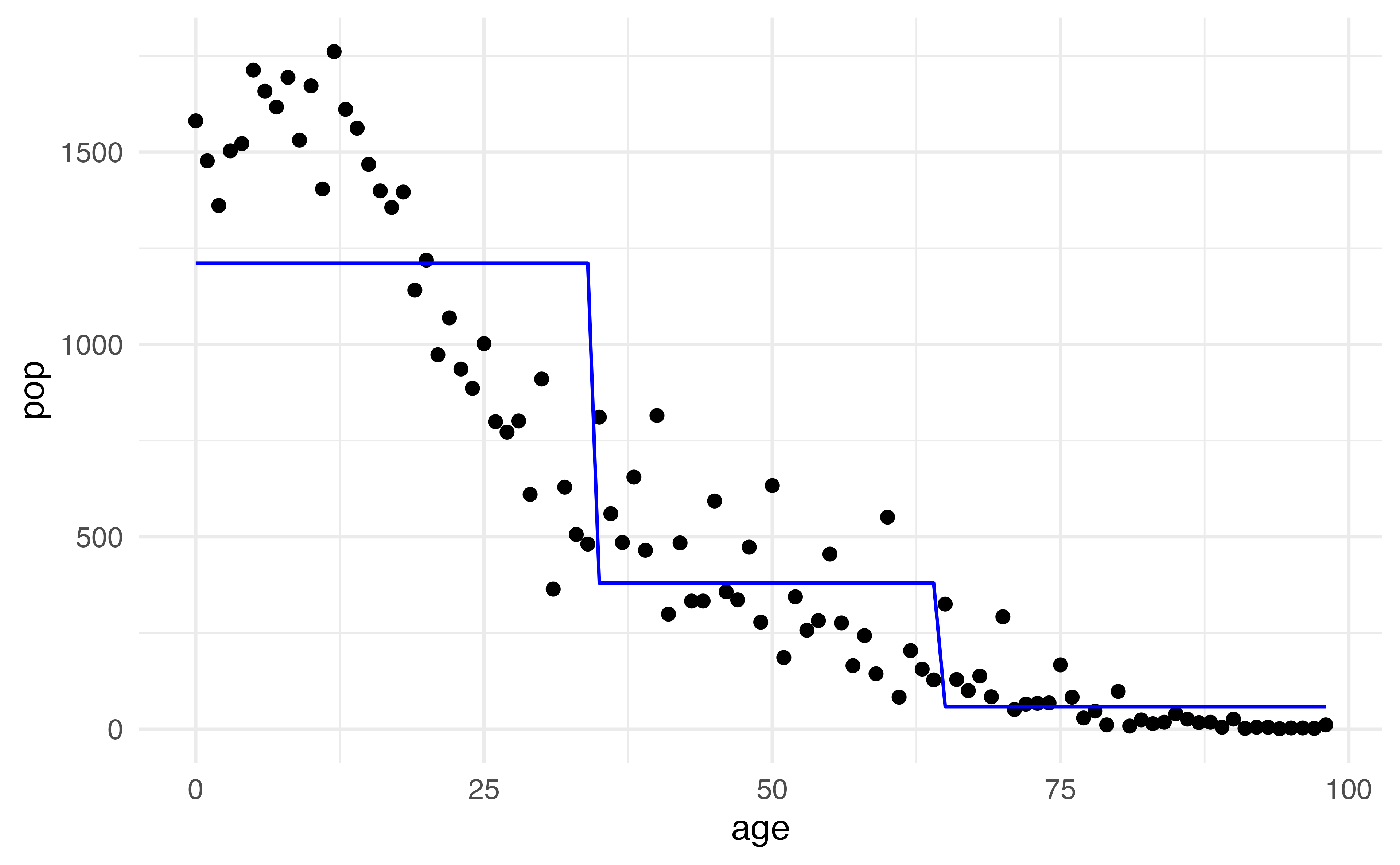
What is the predicted value when \(age = 25\)?

Step functions

\[C_1(X) = I(X < 15), C_2(X) = I(15\leq X<65), C_3(X) = I(X \geq 65)\]

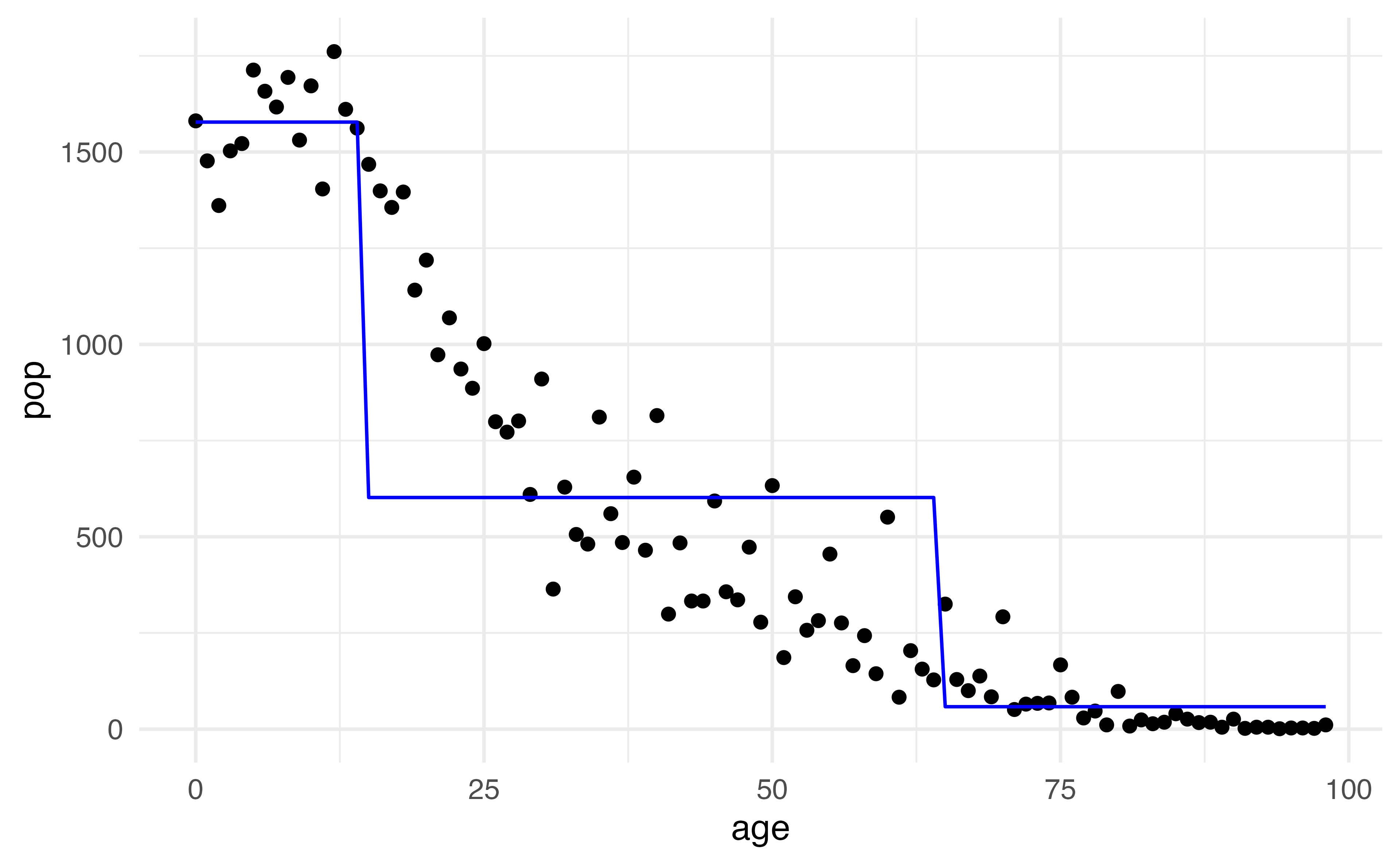
What is the predicted value when \(age = 25\)?

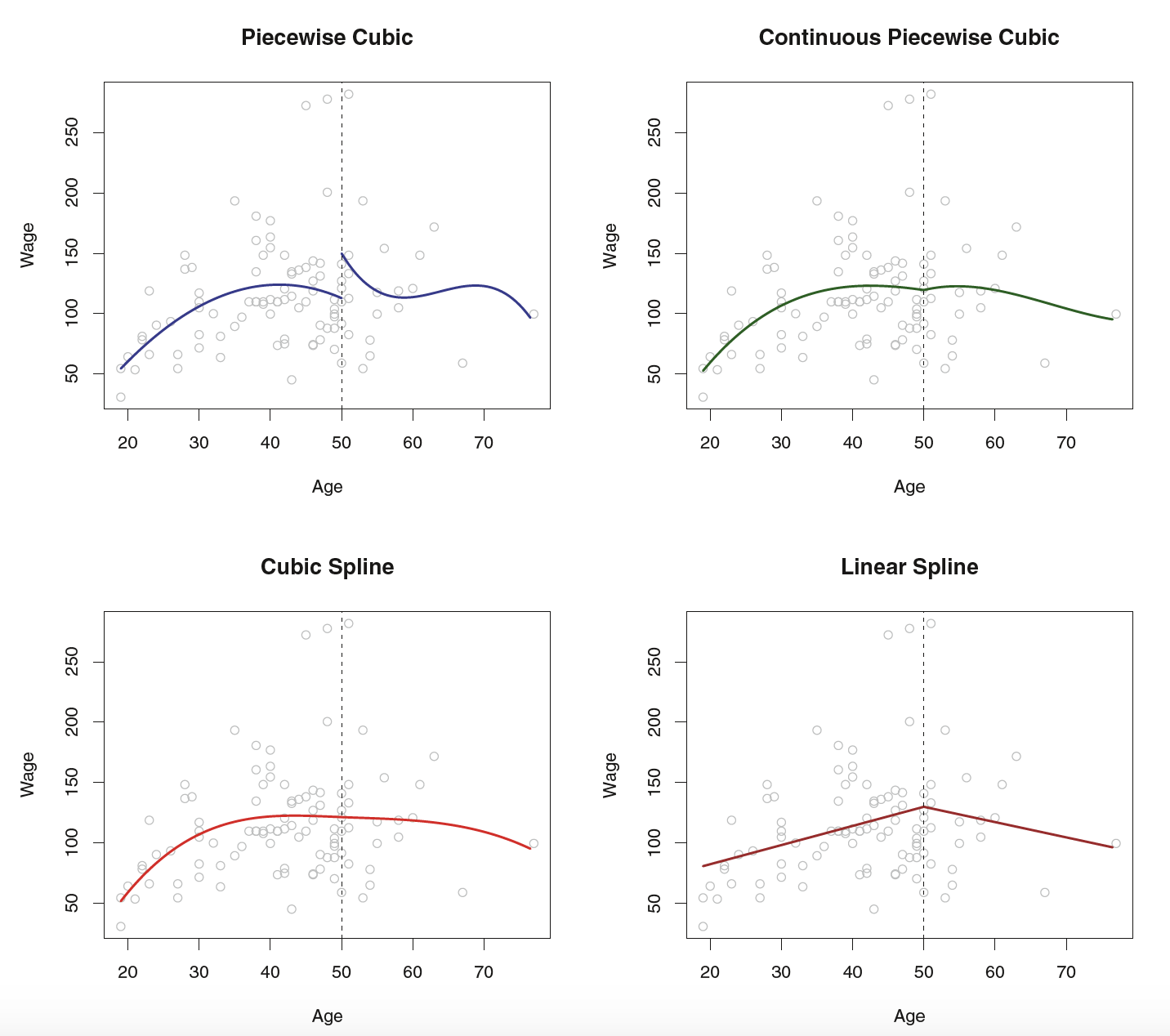
Piecewise polynomials

Instead of a single polynomial in \(X\) over it’s whole domain, we can use different polynomials in regions defined by knots

\[y_i = \begin{cases}\beta_{01}+\beta_{11}x_i + \beta_{21}x^2_i+\beta_{31}x^3_i+\epsilon_i& \textrm{if } x_i < c\\ \beta_{02}+\beta_{12}x_i + \beta_{22}x_i^2 + \beta_{32}x_{i}^3+\epsilon_i&\textrm{if }x_i\geq c\end{cases}\]

What could go wrong here?

  • It would be nice to have constraints (like continuity!)
  • Insert splines!

Linear Splines

A linear spline with knots at \(\xi_k\), \(k = 1,\dots, K\) is a piecewise linear polynomial continuous at each knot

\[y_i = \beta_0 + \beta_1b_1(x_i)+\beta_2b_2(x_i)+\dots+\beta_{K+1}b_{K+1}(x_i)+\epsilon_i\]

  • \(b_k\) are basis functions
  • \(\begin{align}b_1(x_i)&=x_i\\ b_{k+1}(x_i)&=(x_i-\xi_k)_+,k=1,\dots,K\end{align}\)
  • Here \(()_+\) means the positive part
  • \((x_i-\xi_k)_+=\begin{cases}x_i-\xi_k & \textrm{if } x_i>\xi_k\\0&\textrm{otherwise}\end{cases}\)

Application Exercise

Let’s create data set to fit a linear spline with 2 knots: 35 and 65.

x
4
15
25
37
49
66
70
80
  1. Using the data to the left create a new dataset with three variables: \(b_1(x), b_2(x), b_3(x)\)
  2. Write out the equation you would be fitting to estimate the effect on some outcome \(y\) using this linear spline
04:00

Linear Spline

x
4
15
25
37
49
66
70
80

➡️

\(b_1(x)\) \(b_2(x)\) \(b_3(x)\)
4 0 0
15 0 0
25 0 0
37 2 0
49 14 0
66 31 1
70 35 5
80 45 15

Application Exercise

Below is a linear regression model fit to include the 3 bases you just created with 2 knots: 35 and 65. Use the information here to draw the relationship between \(x\) and \(y\).

term estimate std.error statistic p.value
(Intercept) -0.3 0.2 -1.3 0.3
b1 2.0 0.0 231.3 0.0
b2 -2.0 0.0 -130.0 0.0
b3 -3.0 0.0 -116.5 0.0
07:00

Linear Splines

\(b_1(x)\) \(b_2(x)\) \(b_3(x)\)
4 0 0
15 0 0
25 0 0
37 2 0
49 14 0
66 31 1
70 35 5
80 45 15

Linear Splines

Linear Splines

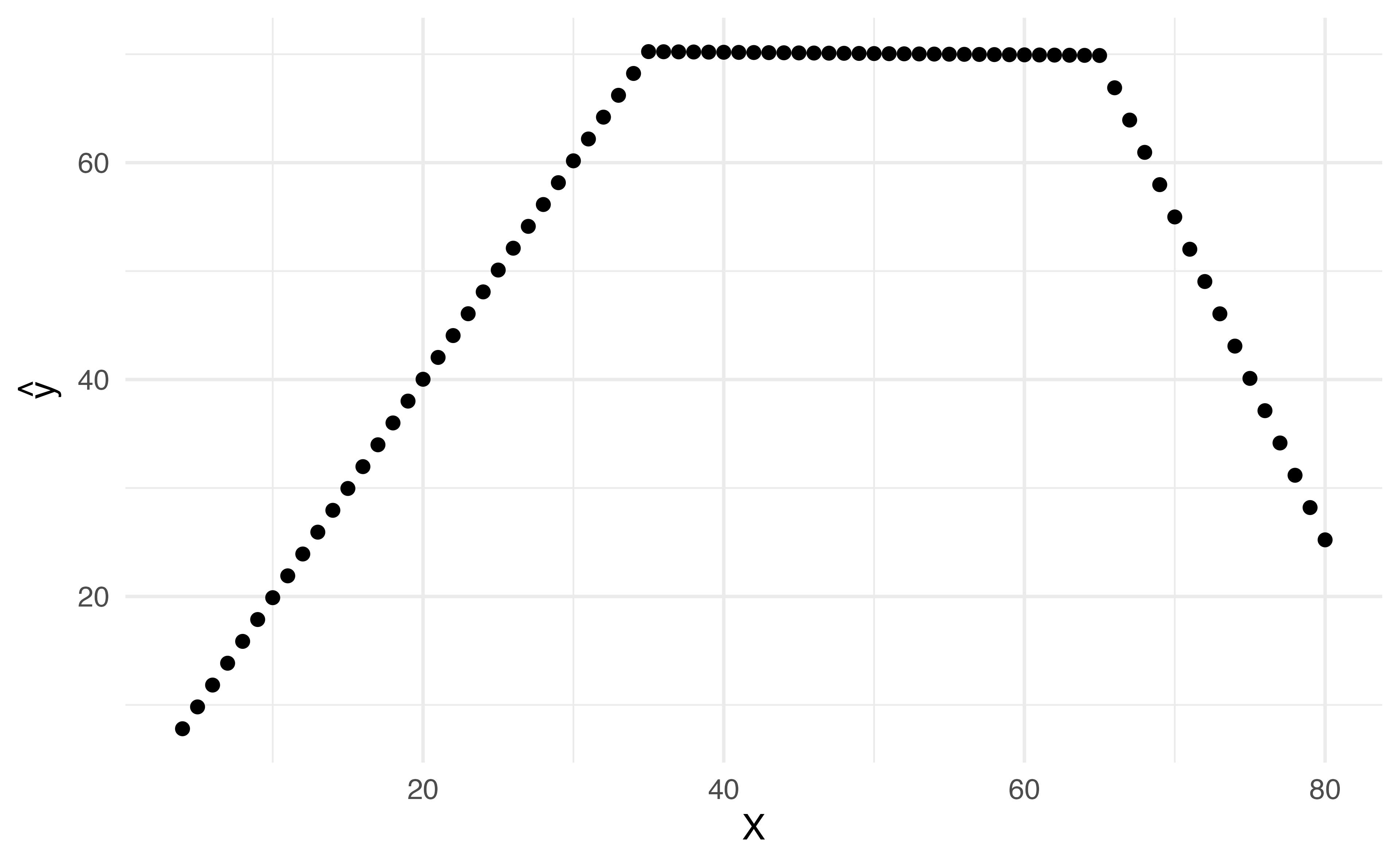
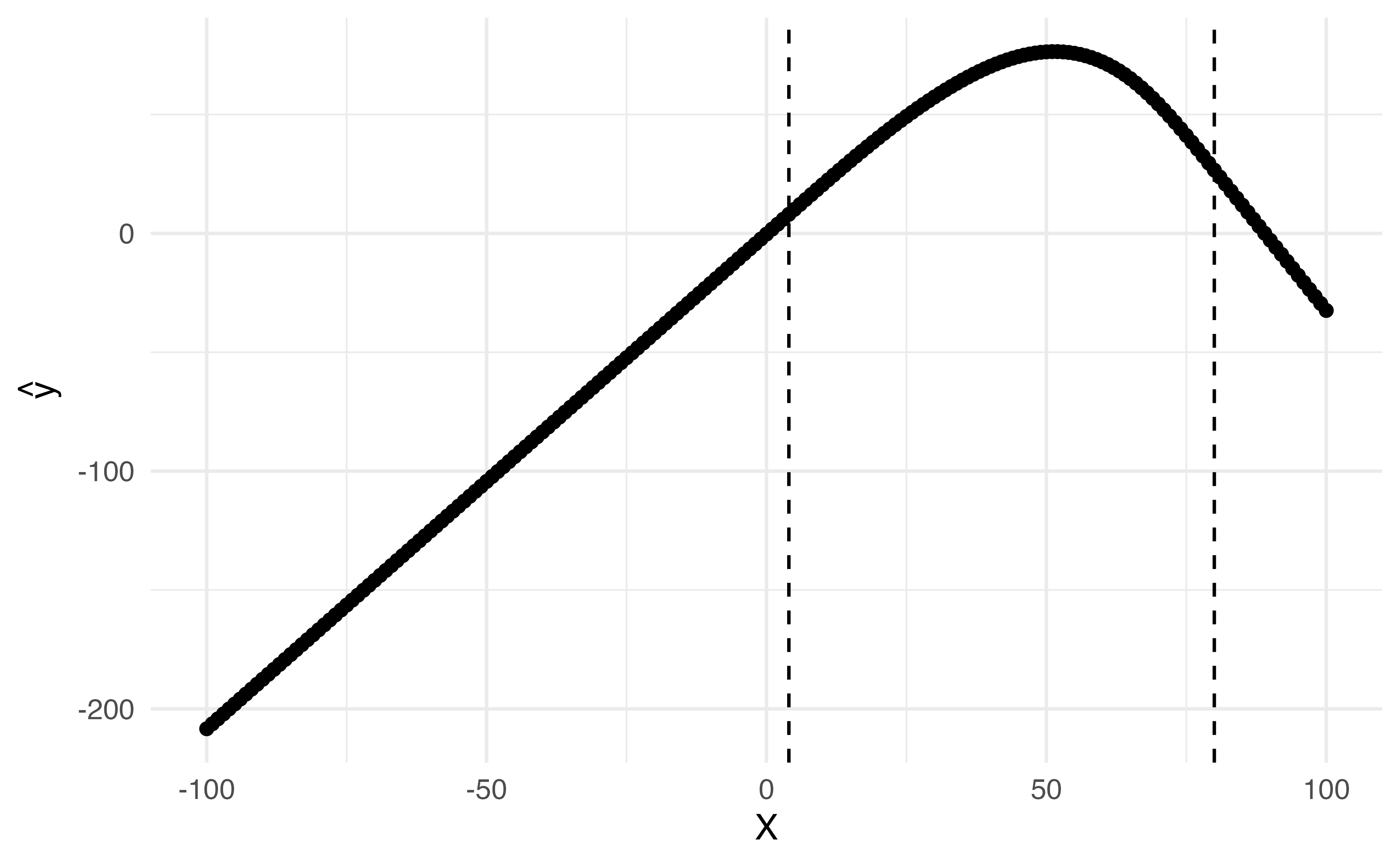
Cubic Splines

A cubic splines with knots at \(\xi_i, k = 1, \dots, K\) is a piecewise cubic polynomial with continuous derivatives up to order 2 at each knot.

Again we can represent this model with truncated power functions

\[y_i = \beta_0 + \beta_1b_1(x_i)+\beta_2b_2(x_i)+\dots+\beta_{K+3}b_{K+3}(x_i) + \epsilon_i\]

\[\begin{align}b_1(x_i)&=x_i\\b_2(x_i)&=x_i^2\\b_3(x_i)&=x_i^3\\b_{k+3}(x_i)&=(x_i-\xi_k)^3_+, k = 1,\dots,K\end{align}\]

where

\[(x_i-\xi_k)^{3}_+=\begin{cases}(x_i-\xi_k)^3&\textrm{if }x_i>\xi_k\\0&\textrm{otherwise}\end{cases}\]

Application Exercise

Let’s create data set to fit a cubic spline with 2 knots: 35 and 65.

x
4
15
25
37
49
66
70
80
  1. Using the data to the left create a new dataset with five variables: \(b_1(x), b_2(x), b_3(x), b_4(x), b_5(x)\)
  2. Write out the equation you would be fitting to estimate the effect on some outcome y using this cubic spline
05:00

Cubic Spline

x
4
15
25
37
49
66
70
80

➡️

b1 b2 b3 b4 b5
4 16 64 0 0
15 225 3375 0 0
25 625 15625 0 0
37 1369 50653 8 0
49 2401 117649 2744 0
66 4356 287496 29791 1
70 4900 343000 42875 125
80 6400 512000 91125 3375

Cubic Spline

term estimate std.error statistic p.value
(Intercept) 1.172 8.282 0.141 0.900
b1 1.520 1.565 0.971 0.434
b2 0.040 0.075 0.528 0.650
b3 -0.001 0.001 -0.855 0.483
b4 0.001 0.002 0.635 0.590
b5 -0.006 0.007 -0.860 0.480

Cubic Splines

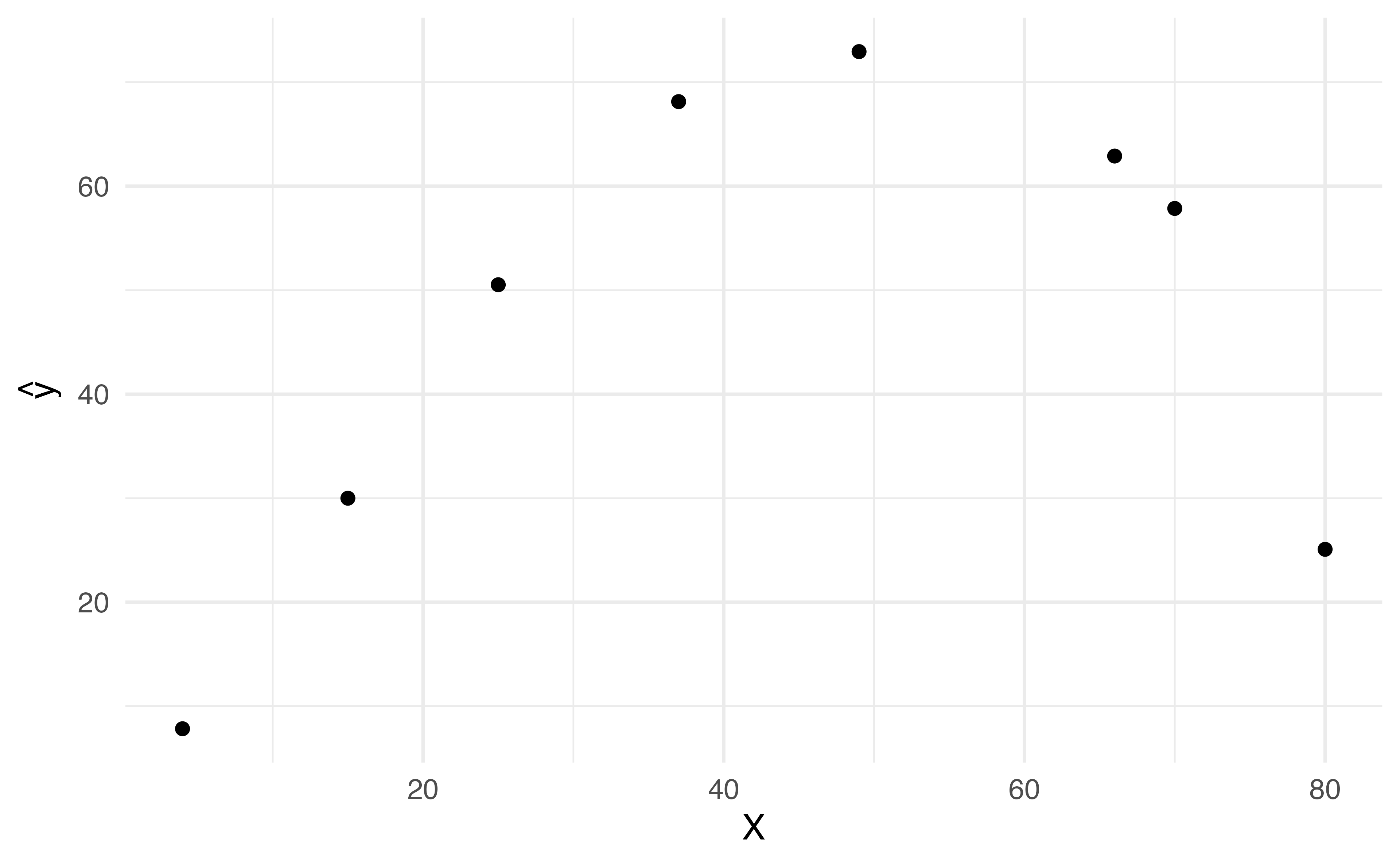
Cubic Splines

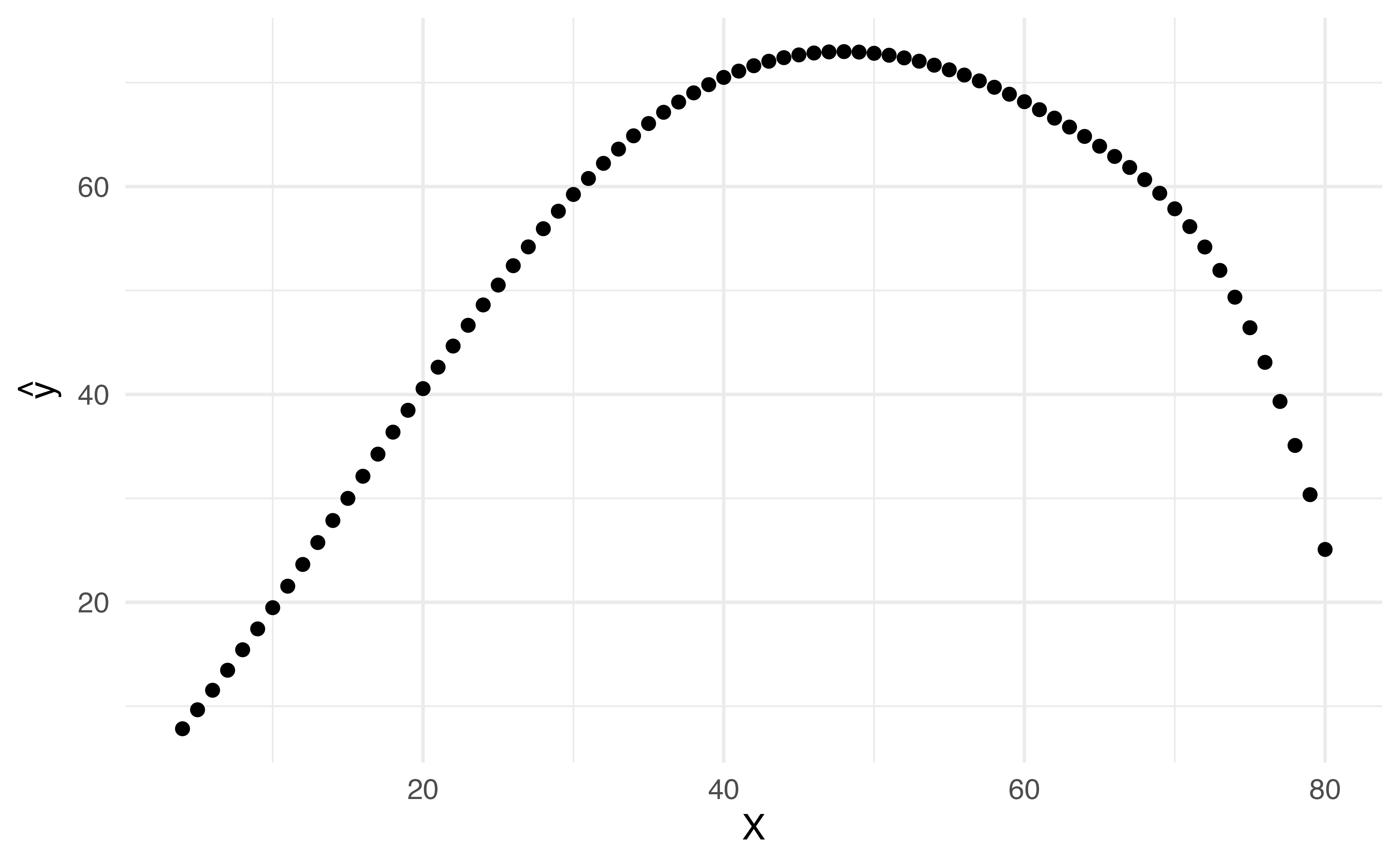
Cubic Splines

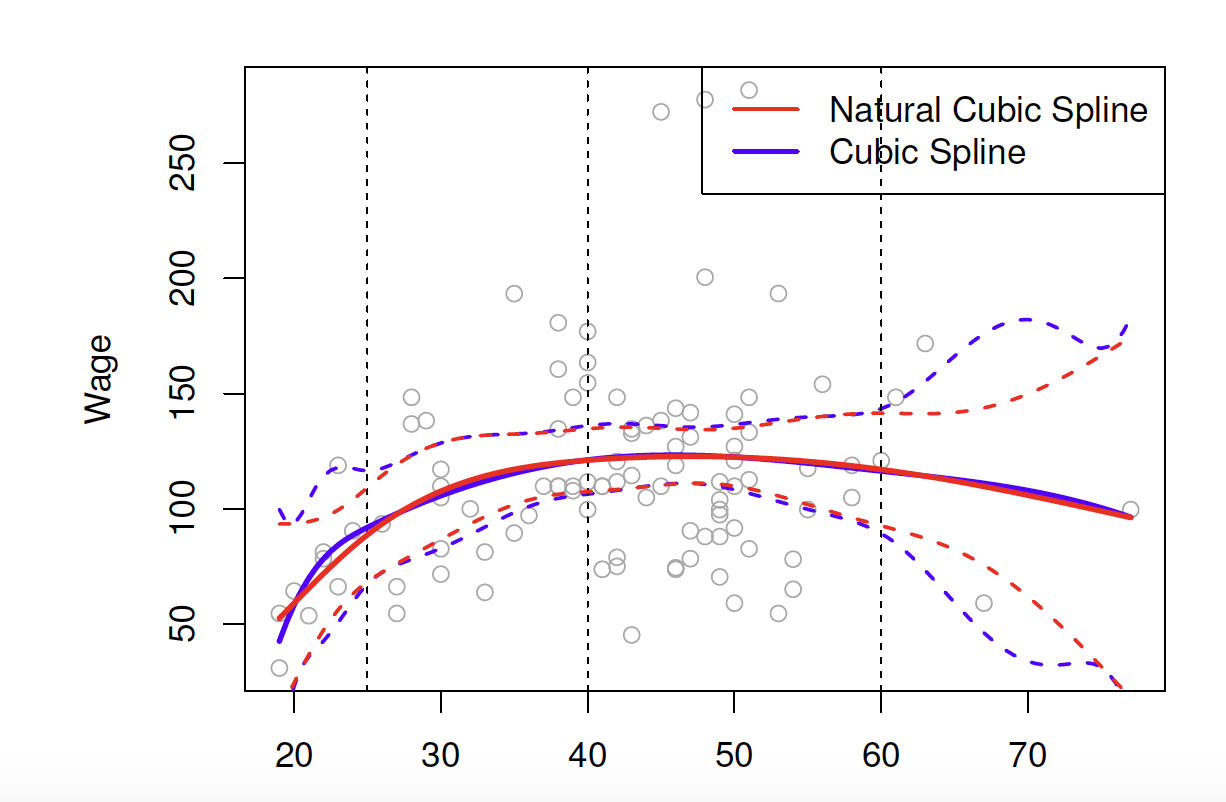
Natural cubic splines

A natural cubic spline extrapolates linearly beyond the boundary knots

This adds 4 extra constraints and allows us to put more internal knots for the same degrees of freedom as a regular cubic spline

Natural Cubic Splines

Natural Cubic Splines

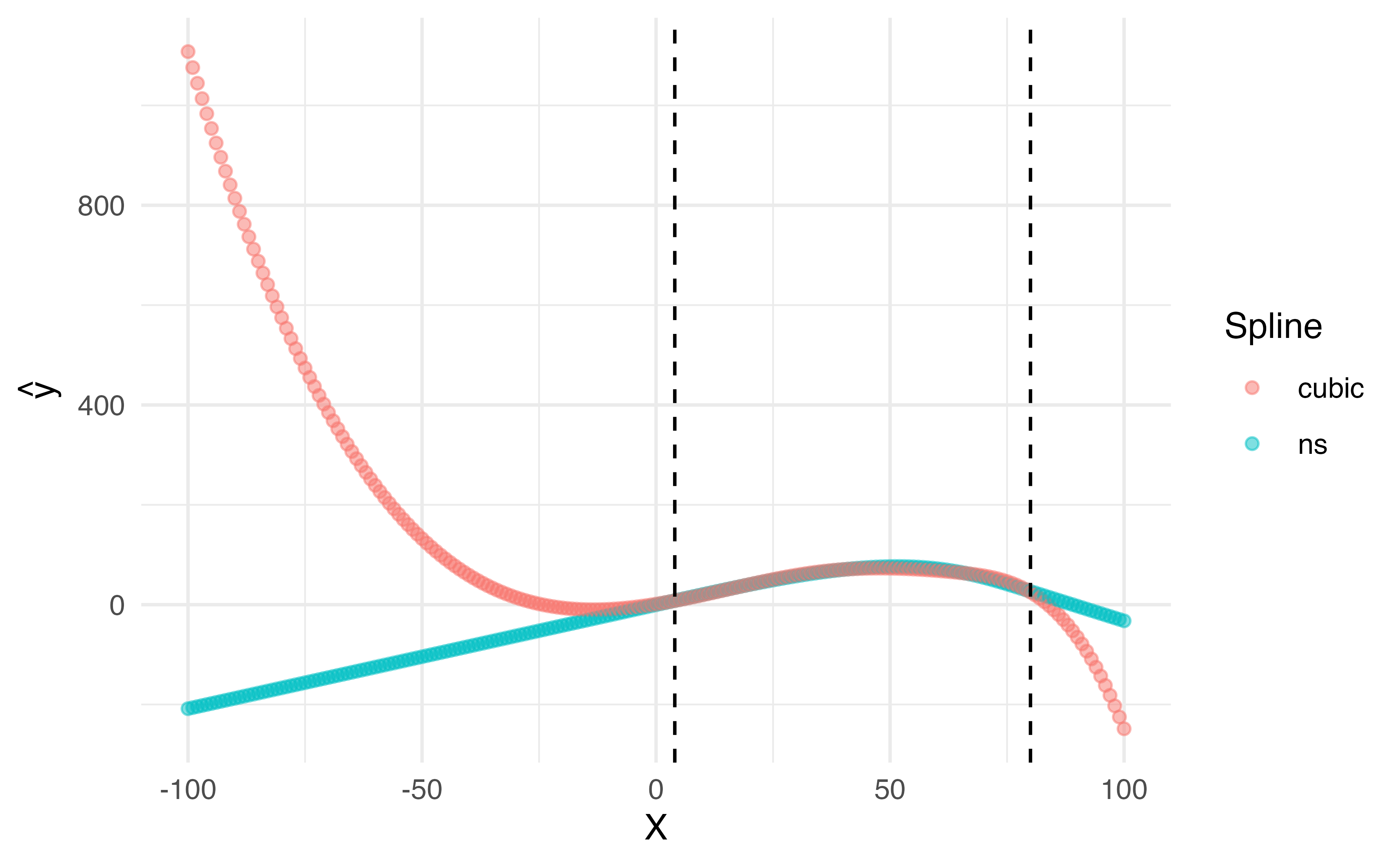
Natural Splines

ggplot(da, aes(x = x, y = value, color = name)) +
  geom_point(alpha = 0.5) + 
  geom_vline(xintercept = c(4, 80), lty = 2) +
  labs(x = "X",
       y = expression(hat(y)),
       color = "Spline")

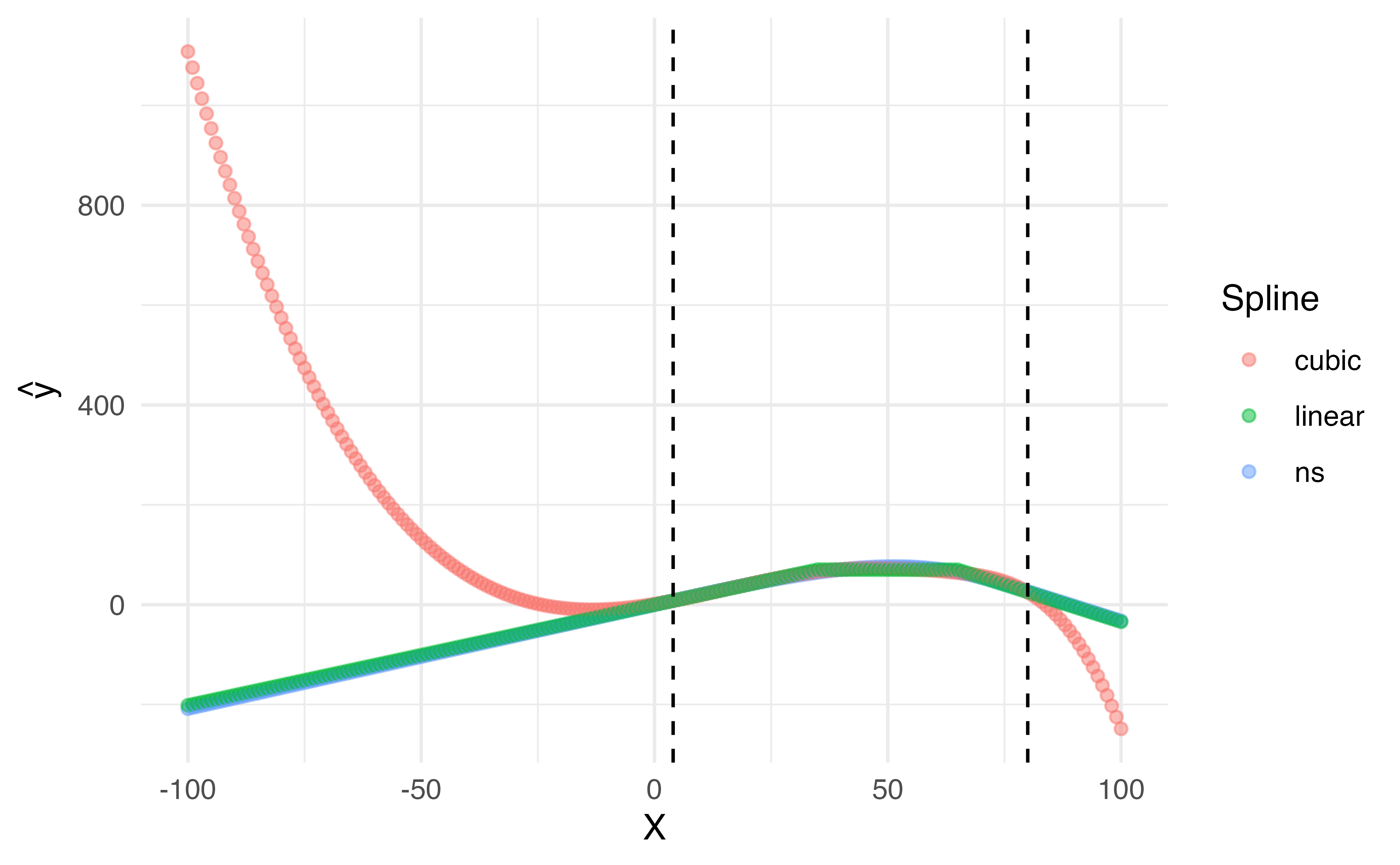
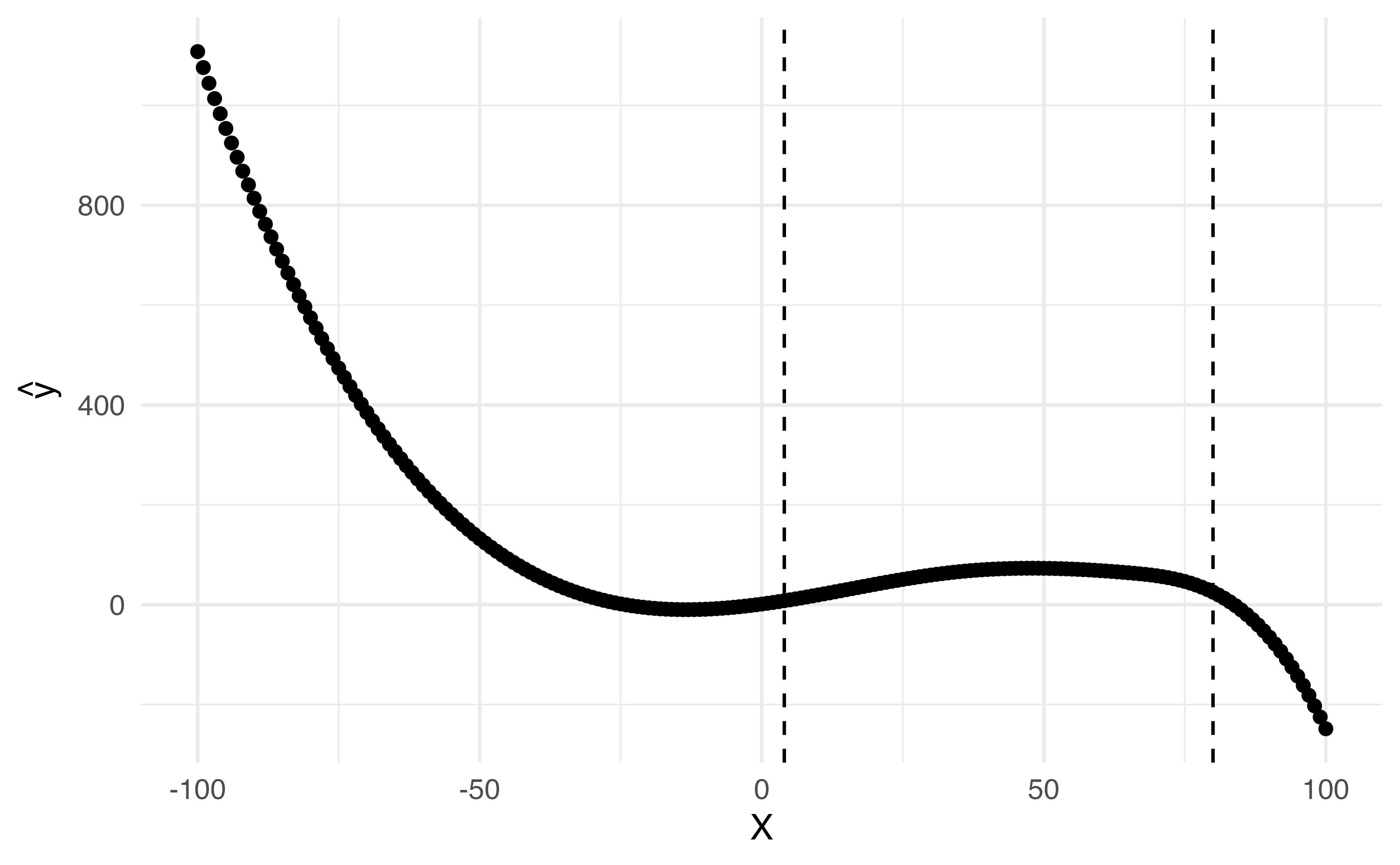
Knot placement

  • One strategy is to decide \(K\) (the number of knots) in advance and then place them at appropriate quantiles of the observed \(X\)
  • A cubic spline with \(K\) knots has \(K+3\) parameters (or degrees of freedom!)
  • A natural spline with \(K\) knots has \(K-1\) degrees of freedom

Knot placement

Here is a comparison of a degree-14 polynomial and natural cubic spline (both have 15 degrees of freedom)

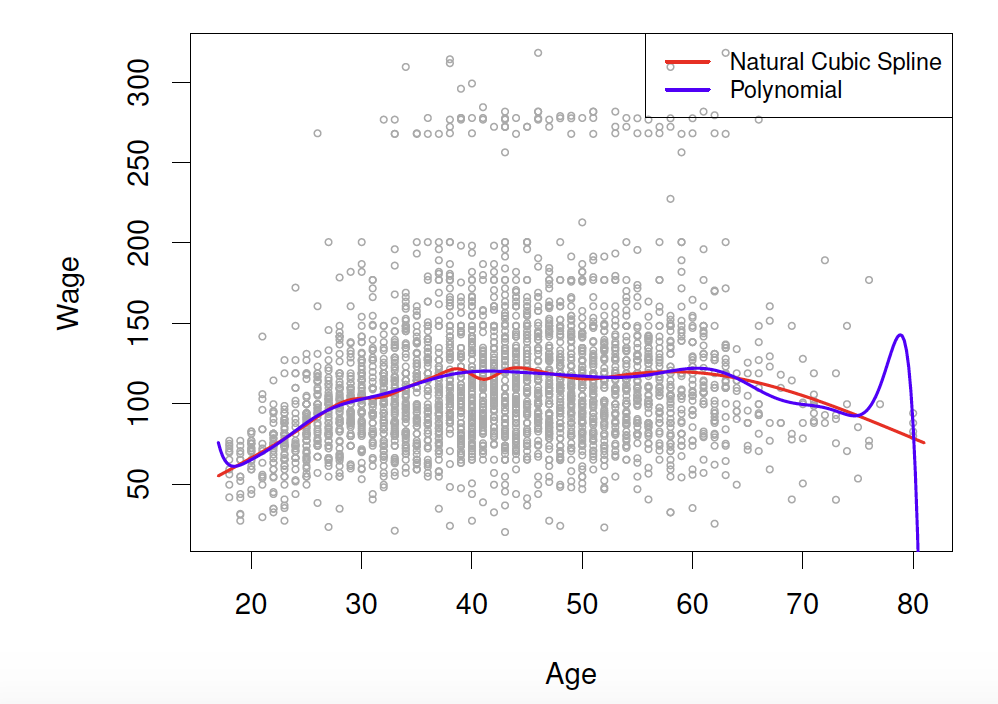
Dr. Lucy D’Agostino McGowan adapted from slides by Hastie & Tibshirani